_mfv2d

_mfv2d#

Internal module which includes functions written in C. These are mostly intended for speed, but some types are written in C for the exprese purpose of making it easier to use in other C functions.

Polynomials#

Since basis require Lagrange polynomials and their derivatives to be computed often, these are implemented in C, where the most efficient algorithms also preserve accuracy for large degrees of these polynomials.

Another commonly required operation is computing Gauss-Legendre-Lobatto nodes and associated integration weights.

mfv2d._mfv2d.lagrange1d(roots: array_like, x: array_like, out: array | None = None, /) → array#

Evaluate Lagrange polynomials.

This function efficiently evaluates Lagrange basis polynomials, defined by

\[\mathcal{L}^n_i (x) = \prod\limits_{j=0, j \neq i}^{n} \frac{x - x_j}{x_i - x_j},\]

where the roots specifies the zeros of the Polynomials \(\{x_0, \dots, x_n\}\).

Parameters:

  • roots (array_like) – Roots of Lagrange polynomials.

  • x (array_like) – Points where the polynomials should be evaluated.

  • out (array, optional) – Array where the results should be written to. If not given, a new one will be created and returned. It should have the same shape as x, but with an extra dimension added, the length of which is len(roots).

Returns:

Array of Lagrange polynomial values at positions specified by x.

Return type:

array

Examples

This example here shows the most basic use of the function to evaluate Lagrange polynomials. First, let us define the roots.

>>> import numpy as np
>>>
>>> order = 7
>>> roots = - np.cos(np.linspace(0, np.pi, order + 1))

Next, we can evaluate the polynomials at positions. Here the interval between the roots is chosen.

>>> from mfv2d._mfv2d import lagrange1d
>>>
>>> xpos = np.linspace(np.min(roots), np.max(roots), 128)
>>> yvals = lagrange1d(roots, xpos)

Note that if we were to give an output array to write to, it would also be the return value of the function (as in no copy is made).

>>> yvals is lagrange1d(roots, xpos, yvals)
True

True

Now we can plot these polynomials.

>>> from matplotlib import pyplot as plt
>>>
>>> plt.figure()
>>> for i in range(order + 1):
...     plt.plot(
...         xpos,
...         yvals[..., i],
...         label=f"$\\mathcal{{L}}^{{{order}}}_{{{i}}}$"
...     )
>>> plt.gca().set(
...     xlabel="$x$",
...     ylabel="$y$",
...     title=f"Lagrange polynomials of order {order}"
... )
>>> plt.legend()
>>> plt.grid()
>>> plt.show()
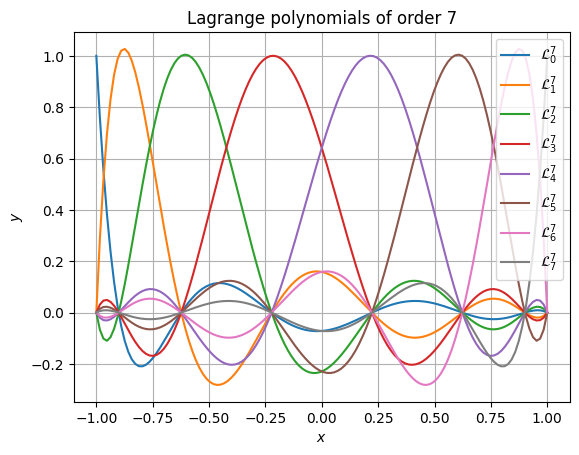
../_images/_mfv2d_3_0.png

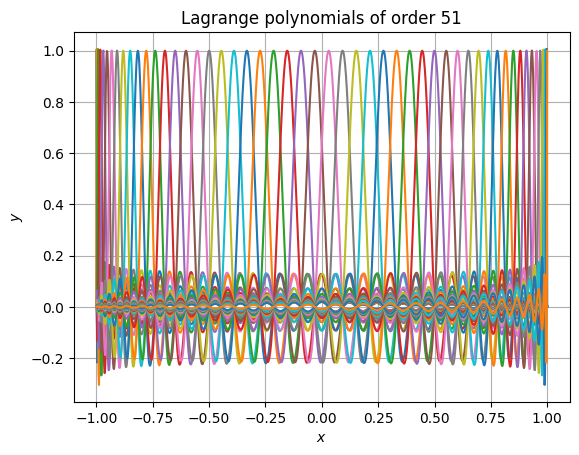
Accuracy is retained even at very high polynomial order. The following snippet shows that even at absurdly high order of 51, the results still have high accuracy and don’t suffer from rounding errors. It also performs well (in this case, the 52 polynomials are each evaluated at 1025 points).

>>> from time import perf_counter
>>> order = 51
>>> roots = - np.cos(np.linspace(0, np.pi, order + 1))
>>> xpos = np.linspace(np.min(roots), np.max(roots), 1025)
>>> t0 = perf_counter()
>>> yvals = lagrange1d(roots, xpos)
>>> t1 = perf_counter()
>>> print(f"Calculations took {t1 - t0: e} seconds.")
>>> plt.figure()
>>> for i in range(order + 1):
...     plt.plot(
...         xpos,
...         yvals[..., i],
...         label=f"$\\mathcal{{L}}^{{{order}}}_{{{i}}}$"
...     )
>>> plt.gca().set(
...     xlabel="$x$",
...     ylabel="$y$",
...     title=f"Lagrange polynomials of order {order}"
... )
>>> # plt.legend() # No, this is too long
>>> plt.grid()
>>> plt.show()

Calculations took  6.473400e-04 seconds.
../_images/_mfv2d_4_1.png
mfv2d._mfv2d.dlagrange1d(roots: array_like, x: array_like, out: array | None = None, /) → array#

Evaluate derivatives of Lagrange polynomials.

This function efficiently evaluates Lagrange basis polynomials derivatives, defined by

\[\frac{d \mathcal{L}^n_i (x)}{d x} = \sum\limits_{j=0,j \neq i}^n \prod\limits_{k=0, k \neq i, k \neq j}^{n} \frac{1}{x_i - x_j} \cdot \frac{x - x_k}{x_i - x_k},\]

where the roots specifies the zeros of the Polynomials \(\{x_0, \dots, x_n\}\).

Parameters:

  • roots (array_like) – Roots of Lagrange polynomials.

  • x (array_like) – Points where the derivatives of polynomials should be evaluated.

  • out (array, optional) – Array where the results should be written to. If not given, a new one will be created and returned. It should have the same shape as x, but with an extra dimension added, the length of which is len(roots).

Returns:

Array of Lagrange polynomial derivatives at positions specified by x.

Return type:

array

Examples

This example here shows the most basic use of the function to evaluate derivatives of Lagrange polynomials. First, let us define the roots.

>>> import numpy as np
>>>
>>> order = 7
>>> roots = - np.cos(np.linspace(0, np.pi, order + 1))

Next, we can evaluate the polynomials at positions. Here the interval between the roots is chosen.

>>> from mfv2d._mfv2d import dlagrange1d
>>>
>>> xpos = np.linspace(np.min(roots), np.max(roots), 128)
>>> yvals = dlagrange1d(roots, xpos)

Note that if we were to give an output array to write to, it would also be the return value of the function (as in no copy is made).

>>> yvals is dlagrange1d(roots, xpos, yvals)
True

True

Now we can plot these polynomials.

>>> from matplotlib import pyplot as plt
>>>
>>> plt.figure()
>>> for i in range(order + 1):
...     plt.plot(
...         xpos,
...         yvals[..., i],
...         label=f"${{\\mathcal{{L}}^{{{order}}}_{{{i}}}}}^\\prime$"
...     )
>>> plt.gca().set(
...     xlabel="$x$",
...     ylabel="$y$",
...     title=f"Lagrange polynomials of order {order}"
... )
>>> plt.legend()
>>> plt.grid()
>>> plt.show()
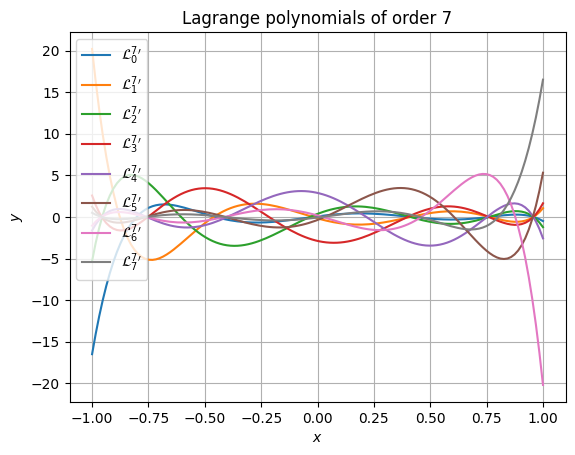
../_images/_mfv2d_8_0.png

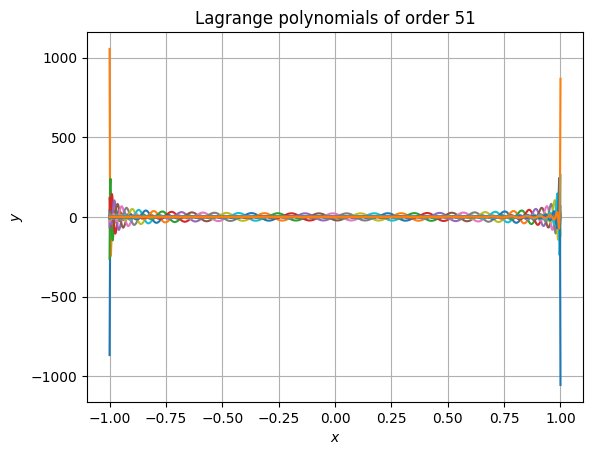
Accuracy is retained even at very high polynomial order. The following snippet shows that even at absurdly high order of 51, the results still have high accuracy and don’t suffer from rounding errors. It also performs well (in this case, the 52 polynomials are each evaluated at 1025 points).

>>> from time import perf_counter
>>> order = 51
>>> roots = - np.cos(np.linspace(0, np.pi, order + 1))
>>> xpos = np.linspace(np.min(roots), np.max(roots), 1025)
>>> t0 = perf_counter()
>>> yvals = dlagrange1d(roots, xpos)
>>> t1 = perf_counter()
>>> print(f"Calculations took {t1 - t0: e} seconds.")
>>> plt.figure()
>>> for i in range(order + 1):
...     plt.plot(
...         xpos,
...         yvals[..., i],
...         label=f"${{\\mathcal{{L}}^{{{order}}}_{{{i}}}}}^\\prime$"
...     )
>>> plt.gca().set(
...     xlabel="$x$",
...     ylabel="$y$",
...     title=f"Lagrange polynomials of order {order}"
... )
>>> # plt.legend() # No, this is too long
>>> plt.grid()
>>> plt.show()

Calculations took  3.005697e-02 seconds.
../_images/_mfv2d_9_1.png
mfv2d._mfv2d.compute_gll(order: int, /, max_iter: int = 10, tol: float = 1e-15) → tuple[array, array]#

Compute Gauss-Legendre-Lobatto integration nodes and weights.

If you are often re-using these, consider caching them.

Parameters:

  • order (int) – Order of the scheme. The number of node-weight pairs is one more.

  • max_iter (int, default: 10) – Maximum number of iterations used to further refine the values.

  • tol (float, default: 1e-15) – Tolerance for stopping the refinement of the nodes.

Returns:

  • array – Array of order + 1 integration nodes on the interval \([-1, +1]\).

  • array – Array of integration weights which correspond to the nodes.

Examples

Gauss-Legendre-Lobatto nodes computed using this function, along with the weights.

>>> import numpy as np
>>> from mfv2d._mfv2d import compute_gll
>>> from matplotlib import pyplot as plt
>>>
>>> n = 5
>>> nodes, weights = compute_gll(n)
>>>
>>> # Plot these
>>> plt.figure()
>>> plt.scatter(nodes, weights)
>>> plt.xlabel("$\\xi$")
>>> plt.ylabel("$w$")
>>> plt.grid()
>>> plt.show()
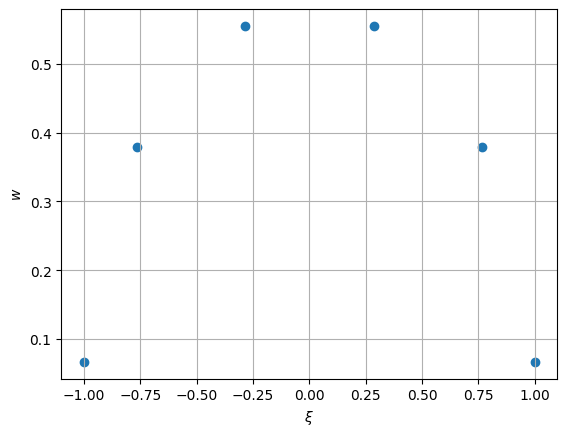
../_images/_mfv2d_10_0.png

Since these are computed in an iterative way, giving a tolerance which is too strict or not allowing for sufficient iterations might cause an exception to be raised to do failiure to converge.

There is also a function to evaluate Legendre polynomials. This is intended to be used for computing projections on Legendre hierarchical basis.

mfv2d._mfv2d.compute_legendre()#

compute_lagrange_polynomials(order: int, positions: array_like, out: array|None = None) -> array Compute Legendre polynomials at given nodes.

Parameters:

  • order (int) – Order of the scheme. The number of node-weight pairs is one more.

  • positions (array_like) – Positions where the polynomials should be evaluated at.

  • out (array, optional) – Output array to write to. If not specified, then a new array is allocated. Must have the exact correct shape (see return value) and data type (double/float64).

Returns:

Array with the same shape as positions parameter, except with an additional first dimension, which determines which Legendre polynomial it is.

Return type:

array

Examples

To quickly illustrate how this function can be used to work with Legendre polynomials, some simple examples are shown.

First things first, the function can be called for any order of polynomials, with about any shape of input array (though if you put too many dimensions you will get an exception). Also, you can supply an optional output parameter, such that an output array need not be newly allocated.

>>> import numpy as np
>>> from mfv2d._mfv2d import compute_legendre
>>>
>>> n = 5
>>> positions = np.linspace(-1, +1, 101)
>>> vals = compute_legendre(n, positions)
>>> assert vals is compute_legendre(n, positions, vals)

The output array will always have the same shape as the input array, with the only difference being that a new axis is added for the first dimension, which can be indexed to distinguish between the different Legendre polynomials.

>>> from matplotlib import pyplot as plt
>>>
>>> fig, ax = plt.subplots(1, 1)
>>>
>>> for i in range(n + 1):
>>>     ax.plot(positions, vals[i, ...], label=f"$y = \\mathcal{{L}}_{{{i:d}}}$")
>>>
>>> ax.set(xlabel="$x$", ylabel="$y$")
>>> ax.grid()
>>> ax.legend()
>>>
>>> fig.tight_layout()
>>> plt.show()
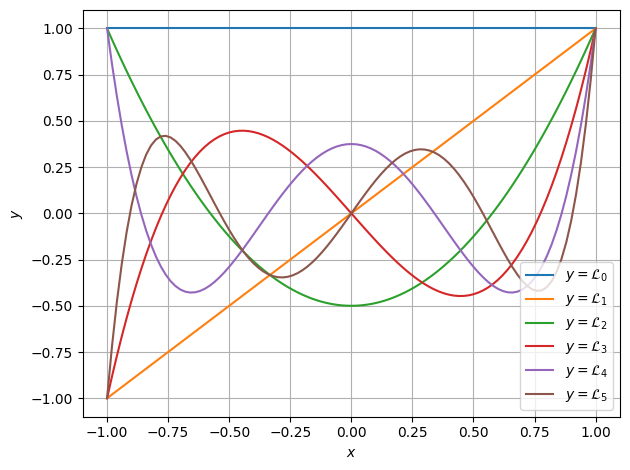
../_images/_mfv2d_12_0.png

Lastly, these polynomials are all orthogonal under the \(L^2\) norm. This can be shown numerically as well.

>>> from mfv2d._mfv2d import IntegrationRule1D
>>>
>>> rule = IntegrationRule1D(n + 1)
>>>
>>> vals = compute_legendre(n, rule.nodes)
>>>
>>> for i1 in range(n + 1):
>>>     p1 = vals[i1, ...]
>>>     for i2 in range(n + 1):
>>>         p2 = vals[i2, ...]
>>>
>>>         integral = np.sum(p1 * p2 * rule.weights)
>>>
>>>         if i1 != i2:
>>>             assert abs(integral) < 1e-16

For conversion of the Legendre basis coefficients into Legendre integral basis coefficients, the function legendre_l2_to_h1_coefficients() is provided.

mfv2d._mfv2d.legendre_l2_to_h1_coefficients(c: array_like, /) → array#

Convert Legendre polynomial coefficients to H1 coefficients.

The \(H^1\) coefficients are based on being expansion coefficients of hierarchical basis which are orthogonal in the \(H^1\) norm instead of in the \(L^2\) norm, which holds for Legendre polynomials instead.

Parameters:

c (array_like) – Coefficients of the Legendre polynomials.

Returns:

Coefficients of integrated Legendre polynomial basis.

Return type:

array

Basis#

In order to define a set of basis, which can be integrated, an integration rule is defined by an IntegrationRule1D. This is essentially wrapped result of compute_gll(), but as an object.

class mfv2d._mfv2d.IntegrationRule1D(order: int)#

Type used to contain integration rule information.

Parameters:

order (int) – Order of integration rule used. Can not be negative.

nodes#

Position of integration nodes on the reference domain [-1, +1] where the integrated function should be evaluated.

Type:

array

order#

order of the rule

Type:

int

weights#

Weight values by which the values of evaluated function should be multiplied by.

Type:

array

Based on an integration rule, one-dimensional basis can be defined with the Basis1D type. This

class mfv2d._mfv2d.Basis1D(order: int, rule: IntegrationRule1D)#

One-dimensional basis functions collection used for FEM space creation.

Parameters:

  • order (int) – Order of basis used.

  • rule (IntegrationRule1D) – Integration rule for basis creation.

Examples

An example of how these basis might look for a 3-rd order element is shown bellow.

>>> from matplotlib import pyplot
>>> from mfv2d._mfv2d import Basis1D, IntegrationRule1D
>>>
>>> #Make a high order rule to make it easy to visualize
>>> rule = IntegrationRule1D(order=31)
>>> basis = Basis1D(3, rule)

Now the nodal basis can be plotted:

>>> plt.figure()
>>> for i in range(basis.order + 1):
...     plt.plot(basis.rule.nodes, basis.node[i, ...], label=f"$b_{{{i}}}$")
>>> plt.grid()
>>> plt.legend()
>>> plt.xlabel("$\\xi$")
>>> plt.title("Nodal basis")
>>> plt.show()
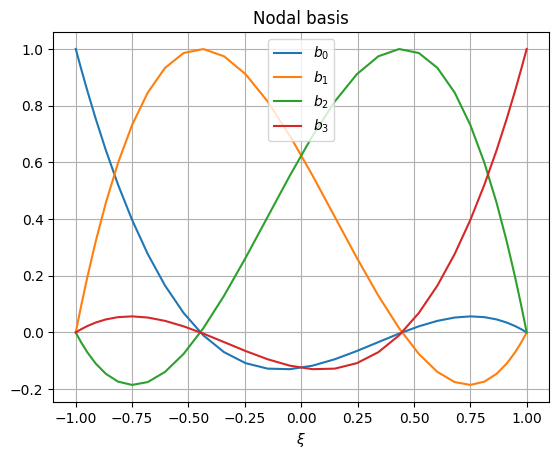
../_images/_mfv2d_15_0.png

Edge basis can also be shown:

>>> plt.figure()
>>> for i in range(basis.order):
...     plt.plot(basis.rule.nodes, basis.edge[i, ...], label=f"$e_{{{i}}}$")
>>> plt.grid()
>>> plt.legend()
>>> plt.xlabel("$\\xi$")
>>> plt.title("Edge basis")
>>> plt.show()
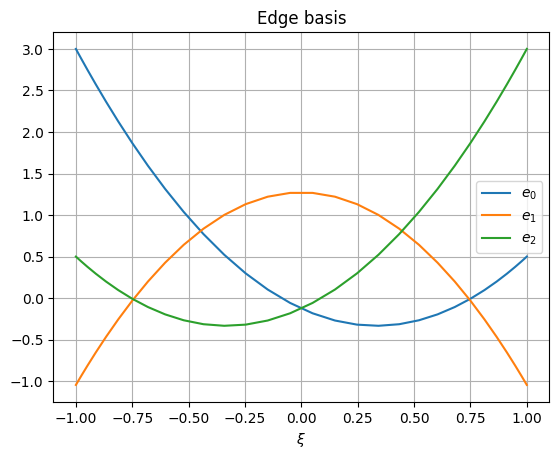
../_images/_mfv2d_16_0.png
edge#

Edge basis values.

Type:

array

node#

Nodal basis values.

Type:

array

order#

Order of the basis.

Type:

int

roots#

Roots of the nodal basis.

Type:

array

rule#

integration rule used

Type:

IntegrationRule1D

Two dimensional basis are constructed from tensor products of one-dimensional basis. As such the Basis2D type is merely a container for two one-dimensional basis.

class mfv2d._mfv2d.Basis2D(basis_xi: Basis1D, basis_eta: Basis1D)#

Two dimensional basis resulting from a tensor product of one dimensional basis.

basis_eta#

Basis used for the Eta direction.

Type:

Basis1D

basis_xi#

Basis used for the Xi direction.

Type:

Basis1D

Topology#

Toplogy information is used when constructing continuity constraints on degrees of freedom. As such, these types allow for very quick and precice lookup of neighbours, computations of duals, and other required operations.

The base building block is the GeoID type, which is a combination of a geometrical object’s index and an indicator of its orientation. Often time functions will allow GeoID arguments to be replaced by 1-based integer index, with its sign indicating orientation.

The index of a GeoID can also be considered invalid. For functions that allow integer along with GeoID this would correspond to passing the value of 0. In that case a value would be equivalent to False in any boolean context.

class mfv2d._mfv2d.GeoID(index: int, reverse=False)#

Type used to identify a geometrical object with an index and orientation.

For many functions which take GeoID argument(s), a 1-based integer index can be used instead, with negative values indicating reverse orientation and the value of 0 indicating an invalid value.

There are also some convenience operators implemented on this type, such as the negation operator to negate orientation, as well as a comparison operator, which allows for comparison of GeoIDs with one another, as well as with int objects to check if they are indeed equivalent.

Parameters:

  • index (int) – Index of the geometrical object. Can not be negative.

  • reverse (any, default: False) – The object’s orientation should be reversed.

Examples

Here are some examples of how these objects can be used:

>>> from mfv2d._mfv2d import GeoID
>>> id1 = GeoID(0)
>>> print(id1)
>>> print(-id1)
>>> -id1 == -1
True

+0
-0

True
index#

Index of the object referenced by id.

Type:

int

reversed#

Is the orientation of the object reversed.

Type:

bool

A Line is a one-dimensional topological object that connects two points with their respective GeoID indices. For a dual line, point indices indicate indices of primal surfaces valid index, with its orientation indicating whether or not the line was in the surface in its positive or negative orientation.

While for primal lines, both points have valid indices, dual lines may not. This happens when a primal line is on the external boundary of the manifold. In that case, the side which has no valid index is comming from bordering on no surfaces on that side.

class mfv2d._mfv2d.Line(begin: GeoID | int, end: GeoID | int)#

Geometrical object, which connects two points.

Lines can also be converted into numpy arrays directly, which essentially converts their beginning and end indices into integers equivalent to their GeoID values.

Parameters:

  • begin (GeoID or int) – ID of the point where the line beings.

  • end (GeoID or int) – ID of the point where the line ends.

Examples

This section just serves to briefly illustrate how a line can be used.

>>> import numpy as np
>>> from mfv2d._mfv2d import Line
>>> ln = Line(1, 2)
>>> print(ln)
>>> # this one has an invalid point
>>> ln2 = Line(0, 3)
>>> print(np.array(ln2))
>>> print(bool(ln2.begin))

(+0 -> +1)
[-2147483648           3]
False
begin#

ID of the point where the line beings.

Type:

GeoID

end#

ID of the point where the line ends.

Type:

GeoID

The last of the topological primitives is the Surface. Surfaces consist of an arbitraty number of lines. This is because dual surfaces corresponding to nodes on the corners of a mesh will in almost all cases have a number of lines different than four.

class mfv2d._mfv2d.Surface(*ids: GeoID | int)#

Two dimensional geometrical object, which is bound by lines.

Since surface can contain a variable number of lines, it has methods based on containers, such as len, which allow for iterations.

Parameters:

*ids (GeoID or int) – Ids of the lines which are the boundary of the surface.

Examples

Some examples of what can be done with surfaces are presented here.

First, the length of the surface can be obtained by using len() build-in.

>>> import numpy as np
>>> from mfv2d._mfv2d import GeoID, Surface
>>>
>>> surf = Surface(1, 2, 3, -4)
>>> len(surf)
4

4

Next, the surface can be iterated over:

>>> for gid in surf:
...     print(gid)

+0
+1
+2
-3

The surface can also be converted into a numpy array directly.

>>> print(np.array(surf))

[ 1  2  3 -4]

Surfaces can together form a Manifold2D object. This is a collection of surfaces which supports most of needed topological operations. It is used for obtaining connectivity of the top level surfaces. As such, it is used in Mesh type.

class mfv2d._mfv2d.Manifold2D#

Two dimensional manifold consisting of surfaces made of lines. .. rubric:: Examples

This is an example of how a manifold may be used:

>>> import numpy as np
>>> from mfv2d._mfv2d import Manifold2D, Surface, Line, GeoID
>>>
>>> triangle = Manifold2D.from_regular(
...     3,
...     [Line(1, 2), Line(2, 3), Line(1, 3)],
...     [Surface(1, 2, -3)],
... )
>>> print(triangle)

Manifold2D(3 points, 3 lines, 1 surfaces)

The previous case only had one surface. In that case, or if all surface have the same number of lines, the class method Manifold2D.from_regular() can be used. If the surface do not have the same number of lines, that can not be used. Instead, the Manifold2D.from_irregular() class method should be used.

>>> house = Manifold2D.from_irregular(
...     5,
...     [
...         (1, 2), (2, 3), (3, 4), (4, 1), #Square
...         (1, 5), (5, 2), # Roof
...     ],
...     [
...         (1, 2, 3, 4), # Square
...         (-1, 5, 6),   # Triangle
...     ]
... )
>>> print(house)

Manifold2D(5 points, 6 lines, 2 surfaces)

From these manifolds, surfaces or edges can be querried back. This is mostly useful when the dual is also computed, which allows to obtain information about neighbouring objects. For example, if we want to know what points are neighbours of point with index 2, we would do the following:

>>> pt_id = GeoID(1, 0)
>>> dual = house.compute_dual() # Get the dual manifold
>>> # Dual surface corresponding to primal point 1
>>> dual_surface = dual.get_surface(pt_id)
>>> print(dual_surface)
>>> for line_id in dual_surface:
...     if not line_id:
...         continue
...     primal_line = house.get_line(line_id)
...     if primal_line.begin == pt_id:
...         pt = primal_line.end
...     else:
...         assert primal_line.end == pt_id
...         pt = primal_line.begin
...     print(f"Point {pt_id} neighbours point {pt}")

(-0 -> +1 -> -5 ->)
Point +1 neighbours point +0
Point +1 neighbours point +2
Point +1 neighbours point +4
compute_dual() → Manifold2D#

Compute the dual to the manifold.

A dual of each k-dimensional object in an n-dimensional space is a (n-k)-dimensional object. This means that duals of surfaces are points, duals of lines are also lines, and that the duals of points are surfaces.

A dual line connects the dual points which correspond to surfaces which the line was a part of. Since the change over a line is computed by subtracting the value at the beginning from that at the end, the dual point which corresponds to the primal surface where the primal line has a positive orientation is the end point of the dual line and conversely the end dual point is the one corresponding to the surface which contained the primal line in the negative orientation. Since lines may only be contained in a single primal surface, they may have an invalid ID as either their beginning or their end. This can be used to determine if the line is actually a boundary of the manifold.

A dual surface corresponds to a point and contains dual lines which correspond to primal lines, which contained the primal point of which the dual surface is the result of. The orientation of dual lines in this dual surface is positive if the primal line of which they are duals originated in the primal point in question and negative if it was their end point.

Returns:

Dual manifold.

Return type:

Manifold2D

dimension#

Dimension of the manifold.

Type:

int

classmethod from_irregular(n_points: int, line_connectivity: array_like, surface_connectivity: Sequence[array_like]) → Self#

Create Manifold2D from surfaces with non-constant number of lines.

Parameters:

  • n_points (int) – Number of points in the mesh.

  • line_connectivity ((N, 2) array_like) – Connectivity of points which form lines in 0-based indexing.

  • surface_connectivity (Sequence of array_like) – Sequence of arrays specifying connectivity of mesh surfaces in 1-based indexing, where a negative value means that the line’s orientation is reversed.

Returns:

Two dimensional manifold.

Return type:

Self

classmethod from_regular(n_points: int, line_connectivity: array_like, surface_connectivity: array_like) → Self#

Create Manifold2D from surfaces with constant number of lines.

Parameters:

  • n_points (int) – Number of points in the mesh.

  • line_connectivity ((N, 2) array_like) – Connectivity of points which form lines in 0-based indexing.

  • surface_connectivity (array_like) – Two dimensional array-like object specifying connectivity of mesh surfaces in 1-based indexing, where a negative value means that the line’s orientation is reversed.

Returns:

Two dimensional manifold.

Return type:

Self

get_line(index: int | GeoID, /) → Line#

Get the line from the mesh.

Parameters:

index (int or GeoID) – Id of the line to get in 1-based indexing or GeoID. If negative, the orientation will be reversed.

Returns:

Line object corresponding to the ID.

Return type:

Line

get_surface(index: int | GeoID, /) → Surface#

Get the surface from the mesh.

Parameters:

index (int or GeoID) – Id of the surface to get in 1-based indexing or GeoID. If negative, the orientation will be reversed.

Returns:

Surface object corresponding to the ID.

Return type:

Surface

n_lines#

Number of lines in the mesh.

n_points#

Number of points in the mesh.

n_surfaces#

Number of surfaces in the mesh.

For hierarchical refinement, individual surfaces of the manifold can be subdivided into smaller sub-surfaces. Dealing with this hierarchy id done with the Mesh type, which was written in C because doing it purely in Python was something I tried to code about three times already, but did not end up working, and this is much nicer with C’s union.

class mfv2d._mfv2d.Mesh(primal: Manifold2D, dual: Manifold2D, corners: array, orders: array, boundary: array)#

Mesh containing topology, geometry, and discretization information.

Parameters:

  • primal (Manifold2D) – Primal topology manifold.

  • dual (Manifold2D) – Dual topology manifold.

  • corners ((N, 4, 2) array) – Array of element corners.

  • orders ((N, 2) array) – Array of element orders.

  • boundary ((N,) array) – Array of boundary edge indices.

boundary_indices#

Indices of the boundary elements.

Type:

array

copy() → Mesh#

Create a copy of the mesh.

Returns:

Copy of the mesh.

Return type:

Mesh

dual#

Dual manifold topology.

Type:

mfv2d._mfv2d.Manifold2d

element_count#

Number of elements in the mesh.

Type:

int

get_element_children(idx: SupportsIndex, /) → tuple[int, int, int, int] | None#

Get indices of element’s children.

Parameters:

idx (SupportsIndex) – Index of the element to get the children for.

Returns:

If the element has children, their indices are returned in the order bottom left, bottom right, top right, and top left. If the element is a leaf element and has no parents, None is returned.

Return type:

(int, int, int, int) or None

get_element_depth(idx: SupportsIndex, /) → int#

Check how deep the element is in the hierarchy.

Parameters:

idx (SupportsIndex) – Index of the element element to check.

Returns:

Number of ancestors of the element.

Return type:

int

get_element_parent(idx: SupportsIndex, /) → int | None#

Get the index of the element’s parent or None if it is a root element.

Parameters:

idx (SupportsIndex) – Index of the element to get the parent from.

Returns:

If the element has a parent, its index is returned. If the element is a root element and has no parent, None is returned instead.

Return type:

int or None

get_leaf_corners(idx: SupportsIndex, /) → npt.NDArray[np.double]#

Get corners of the leaf element.

Parameters:

idx (SupportsIndex) – Index of the leaf element to get the orders for.

Returns:

Corners of the element in the counter-clockwise order, starting at the bottom left corner.

Return type:

(4, 2) array

get_leaf_indices() → npt.NDArray[np.uintc]#

Get indices of leaf elements.

Returns:

Indices of leaf elements.

Return type:

(N,) array

get_leaf_orders(idx: SupportsIndex, /) → tuple[int, int]#

Get orders of the leaf element.

Parameters:

idx (SupportsIndex) – Index of the leaf element to get the orders for.

Returns:

Orders of the leaf element in the first and second direction.

Return type:

(int, int)

leaf_count#

Number of leaf elements in the mesh.

Type:

int

primal#

Primal manifold topology.

Type:

mfv2d._mfv2d.Manifold2d

set_leaf_orders(idx: SupportsIndex, /, order_1: int, order_2: int) → None#

Set orders of a leaf element.

Parameters:

  • idx (SupportsIndex) – Index of the leaf element to set.

  • order_1 (int) – New order of the leaf in the first dimension.

  • order_2 (int) – New order of the leaf in the second dimension.

split_breath_first(maximum_depth: int, predicate: Callable, *args, **kwargs) → Mesh#

Split leaf elements based on a predicate in a breath-first approach.

Parameters:

  • maximum_depth (int) – Maximum number of levels of division allowed.

  • predicate (Callable) – Predicate to use for determining if the element should be split. It will always be given the mesh as the first argument and the ID of the element as its second argument. If the element should not be split, the function should return None, otherwise it should return orders for all four newly created elements.

  • *args – Arguments passed to the predicate function.

  • **kwargs – Keyword arguments passed to the predicate function.

Returns:

Mesh with refined elements.

Return type:

Mesh

split_depth_first(maximum_depth: int, predicate: Callable, *args, **kwargs) → Mesh#

Split leaf elements based on a predicate in a depth-first approach.

Parameters:

  • maximum_depth (int) – Maximum number of levels of division allowed.

  • predicate (Callable) – Predicate to use for determining if the element should be split. It will always be given the mesh as the first argument and the ID of the element as its second argument. If the element should not be split, the function should return None, otherwise it should return orders for all four newly created elements.

  • *args – Arguments passed to the predicate function.

  • **kwargs – Keyword arguments passed to the predicate function.

Returns:

Mesh with refined elements.

Return type:

Mesh

split_element(idx: SupportsIndex, /, orders_bottom_left: tuple[int, int], orders_bottom_right: tuple[int, int], orders_top_right: tuple[int, int], orders_top_left: tuple[int, int]) → None#

Split a leaf element into four child elements.

Parameters:

  • idx (SupportsIndex) – Index of the element to split. Must be a leaf.

  • orders_bottom_left ((int, int)) – Orders of the newly created bottom left elements.

  • orders_bottom_right ((int, int)) – Orders of the newly created bottom right elements.

  • orders_top_right ((int, int)) – Orders of the newly created top right elements..

  • orders_top_left ((int, int)) – Orders of the newly created top left elements.

Evaluating Terms#

One of key operations that need to be supported in order to solve a system is either computation of element matrices, or computing what is their product with the current solution vector. The instruction translation and generation is handled by the mfv2d.kforms module, so as far as mfv2d._mfv2d code is concerned, it receives parsed bytecode it just needs to execute.

One of the most important functions in the entire module is compute_element_matrix(). This can be used to generate individual element matrices for the system, which can then be combined into the global system matrix.

mfv2d._mfv2d.compute_element_matrix(form_orders: Sequence[int], expressions: _CompiledCodeMatrix, corners: NDArray, vector_fields: Sequence[npt.NDArray[np.float64]], basis: Basis2D, stack_memory: int = 1 << 24) → NDArray#

Compute a single element matrix.

Parameters:

  • form_orders (Sequence of int) – Orders of differential forms for the degrees of freedom. Must be between 0 and 2.

  • expressions – Compiled bytecode to execute.

  • corners ((4, 2) array) – Array of corners of the element.

  • vector_fields (Sequence of arrays) – Vector field arrays as required for interior product evaluations.

  • basis (Basis2D) – Basis functions with integration rules to use.

  • stack_memory (int, default: 1 << 24) – Amount of memory to use for the evaluation stack.

Returns:

Element matrix for the specified system.

Return type:

array

If evaluation of the product of the solution vector with the matrix is needed, instead of computing it with compute_element_matrix(), it can instead be obtained from compute_element_vector(). This is especially useful for non-linear terms, since they would require matrices to be evaulated at every iteration.

mfv2d._mfv2d.compute_element_vector(form_orders: Sequence[int], expressions: _CompiledCodeMatrix, corners: array, vector_fields: Sequence[array], basis: Basis2D, solution: array, stack_memory: int = 1 << 24) → array#

Compute a single element forcing.

Parameters:

  • form_orders (Sequence of int) – Orders of differential forms for the degrees of freedom. Must be between 0 and 2.

  • expressions – Compiled bytecode to execute.

  • corners ((4, 2) array) – Array of corners of the element.

  • vector_fields (Sequence of arrays) – Vector field arrays as required for interior product evaluations.

  • basis (Basis2D) – Basis functions with integration rules to use.

  • solution (array) – Array with degrees of freedom for the element.

  • stack_memory (int, default: 1 << 24) – Amount of memory to use for the evaluation stack.

Returns:

Element vector for the specified system.

Return type:

array

Projections#

There are two functions related to projection of degrees of freedom. These are concerned with two different types of projection. First is the less intuitive one and is the the projection between primal and dual degrees of freedom. This is done by the compute_element_mass_matrix() function, which does exactly as its name would suggest.

mfv2d._mfv2d.compute_element_mass_matrix(form_orders: Sequence[UnknownFormOrders], corners: array, basis: Basis2D, inverse: bool = False) → array#

Compute mass matrix for a given element.

Parameters:

  • form_order (UnknownFormOrder) – Order of the form for which the mass matrix should be computed.

  • corners ((4, 2) array) – Array of corner points of the element.

  • basis (Basis2D) – Basis used for the test and sample space.

  • inverse (bool, default: False) – Should the inverse of the matrix be computed instead of its value directly.

Returns:

Mass matrix (or its inverse if specified) for the appropriate form.

Return type:

array

The second kind of projection is from a lower order Basis2D to higher order Basis2D or vice versa. This is performed by the matrices computed by compute_element_projector(). If its resulting projection matirx is transposed, it will instead act as the projector for dual degrees of freedom.

mfv2d._mfv2d.compute_element_projector(form_orders: Sequence[UnknownFormOrders], corners: array, basis_in: Basis2D, basis_out: Basis2D) → tuple[array]:#

Compute \(L^2\) projection from one space to another.

Projection takes DoFs from primal space of the first and takes them to the primal space of the other.

Parameters:

  • form_orders (Sequence of UnknownFormOrder) – Sequence of orders of forms which are to be projected.

  • corners ((4, 2) array) – Array of corner points of the element.

  • basis_in (Basis2D) – Basis from which the DoFs should be taken.

  • basis_out (Basis2D) – Basis to which the DoFs are taken.

Returns:

Tuple where each entry is the respective projection matrix for that form.

Return type:

tuple of square arrays

Contents