Meshing a Circle

This example shows how a simple circular mesh can be created using rmsh. It is also intended to show what incorrect usage may lead to in hopes of being useful when trying to identify errors.

The Setup

First the common setup for plotting has to be made. For this case, it will be done using the matplotlib module, using matplotlib.collections.LineCollection to plot cell boundaries.

from time import perf_counter

import numpy as np
from matplotlib import pyplot as plt
from matplotlib.collections import LineCollection
from rmsh import (
    BoundaryBlock,
    BoundaryCurve,
    BoundaryId,
    Mesh2D,
    MeshBlock,
    SolverConfig,
    create_elliptical_mesh,
)


def plot_mesh(m: Mesh2D) -> None:
    """Show the mesh using matplotlib."""
    x = m.pos_x
    y = m.pos_y
    line_indices = m.lines
    xb = x[line_indices[:, 0]]
    xe = x[line_indices[:, 1]]
    yb = y[line_indices[:, 0]]
    ye = y[line_indices[:, 1]]

    rb = np.stack((xb, yb), axis=1)
    re = np.stack((xe, ye), axis=1)
    c = LineCollection(np.stack((rb, re), axis=1))
    plt.scatter(x, y, s=8, color="red")
    # for idx in range(line_indices.shape[0]):
    #     plt.plot((xb[idx], xe[idx]), (yb[idx], ye[idx]))
    plt.gca().add_collection(c)
    plt.gca().set_aspect("equal")
    plt.xlim(-1.1, +1.1)
    plt.ylim(-1.1, +1.1)
    plt.show()

Simplest

First is the most basic approach. In this case, only a single block is used, with its boundaries being the circumference of the circle that we want to mesh.

def one_block_only(n1: int, n2: int) -> Mesh2D:
    """Mesh a circle with a single block."""
    angle_l = np.linspace(+0 * np.pi / 2, +1 * np.pi / 2, n1)
    angle_b = np.linspace(+1 * np.pi / 2, +2 * np.pi / 2, n2)
    angle_r = np.linspace(+2 * np.pi / 2, +3 * np.pi / 2, n1)
    angle_t = np.linspace(+3 * np.pi / 2, +4 * np.pi / 2, n2)

    cl = BoundaryCurve(np.cos(angle_l), np.sin(angle_l))
    cr = BoundaryCurve(np.cos(angle_r), np.sin(angle_r))
    ct = BoundaryCurve(np.cos(angle_t), np.sin(angle_t))
    cb = BoundaryCurve(np.cos(angle_b), np.sin(angle_b))

    block = MeshBlock(
        "only one",
        {
            BoundaryId.BoundaryWest: cl,
            BoundaryId.BoundaryEast: cr,
            BoundaryId.BoundaryNorth: ct,
            BoundaryId.BoundarySouth: cb,
        },
    )
    t0 = perf_counter()
    m, _, _ = create_elliptical_mesh([block])
    t1 = perf_counter()
    print(f"Meshed in {t1 - t0:g} seconds.")
    return m


# Now let's show it!

plot_mesh(one_block_only(2, 2))

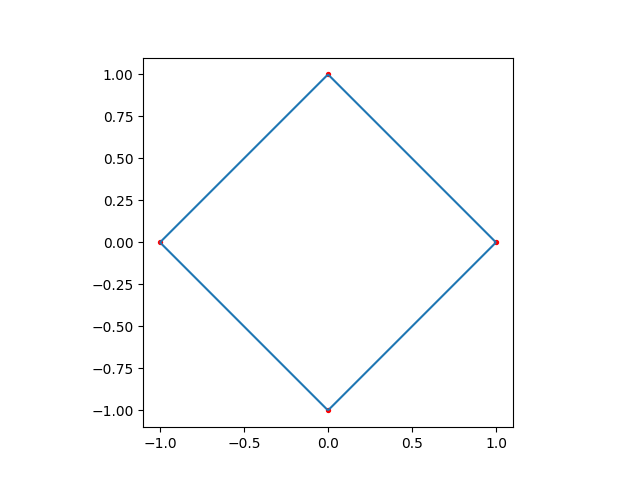
Meshed in 0.00049365 seconds.

plot_mesh(one_block_only(10, 10))

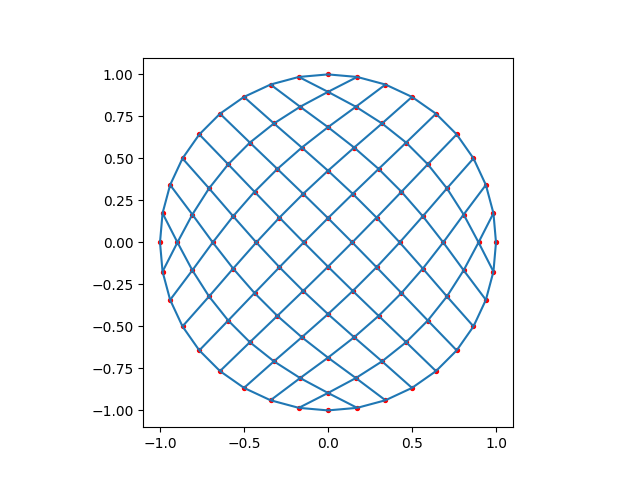
Meshed in 0.000499351 seconds.

plot_mesh(one_block_only(50, 50))

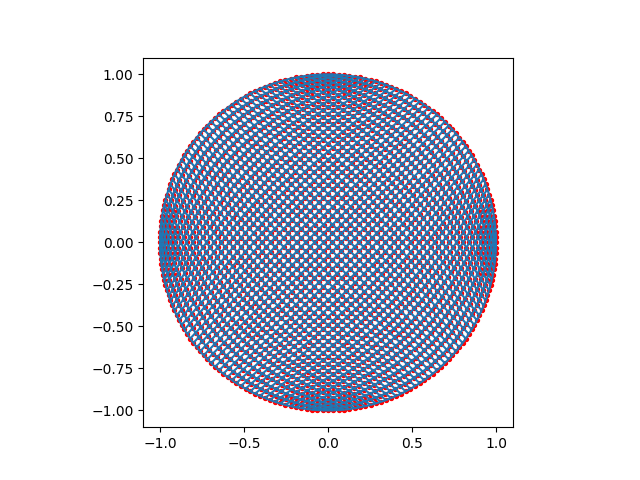
Meshed in 0.00807735 seconds.

Almost the Worst

Next is one worst possible things you can make while meshing: a pair of boundaries, which at no point have a connection with a curve. In this case, the left and right boundaries only need to connect to one another and have no requirement on their position. Top and bottom boundaries each cover half of a circle.

The resulting mesh is very overlapping and very silly looking. If you obtain such a mesh from your meshing, consider checking how you’ve defined the boundaries defined by BoundaryBlock objects.

def self_closed_mesh(n1: int, n2: int) -> Mesh2D:
    """Mesh a circle by self connecting two opposing boundaries."""
    angle_b = np.linspace(-np.pi, 0, n2)
    angle_t = np.linspace(0, +np.pi, n2)

    ct = BoundaryCurve(np.cos(angle_t), np.sin(angle_t))
    cb = BoundaryCurve(np.cos(angle_b), np.sin(angle_b))

    bl = BoundaryBlock("only one", BoundaryId.BoundaryEast, n1)
    br = BoundaryBlock("only one", BoundaryId.BoundaryWest, n1)

    block = MeshBlock(
        "only one",
        {
            BoundaryId.BoundaryWest: bl,
            BoundaryId.BoundaryEast: br,
            BoundaryId.BoundaryNorth: ct,
            BoundaryId.BoundarySouth: cb,
        },
    )

    t0 = perf_counter()
    m, _, _ = create_elliptical_mesh([block])
    t1 = perf_counter()
    print(f"Meshed in {t1 - t0:g} seconds.")
    return m


# Now let's show it!

plot_mesh(self_closed_mesh(2, 2))

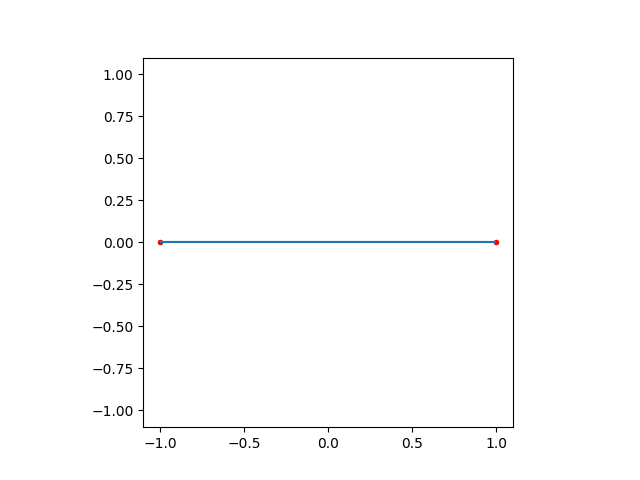
Meshed in 3.8422e-05 seconds.

plot_mesh(self_closed_mesh(10, 10))

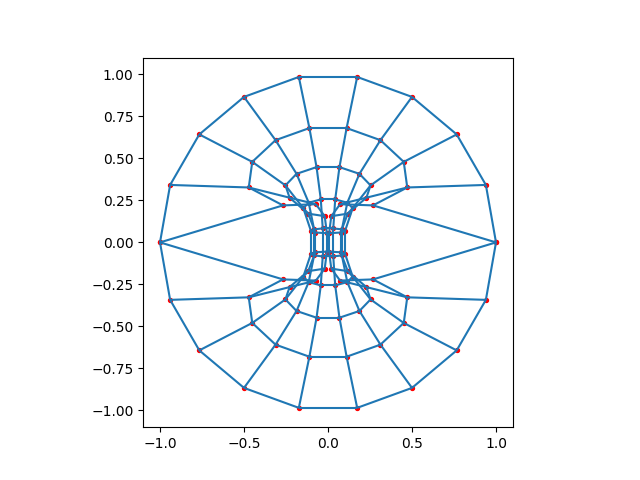
Meshed in 0.000170168 seconds.

plot_mesh(self_closed_mesh(50, 50))

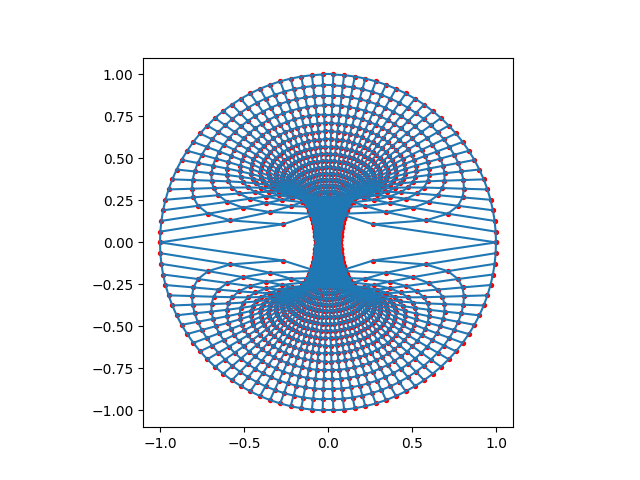
Meshed in 0.0102777 seconds.

Doing it Wrong

A way to make the initial circular mesh better would be to mesh with five blocks, rather than five. However if they are connected incorrectly, the result will be significantly worse.

def four_wierdly_connected_ones(n1: int, n2: int) -> Mesh2D:
    """Mesh in a weird way, where four blocks are used, but weirdly connected."""
    angle_l = np.linspace(+0 * np.pi / 2, +1 * np.pi / 2, n1)
    angle_b = np.linspace(+1 * np.pi / 2, +2 * np.pi / 2, n2)
    angle_r = np.linspace(+2 * np.pi / 2, +3 * np.pi / 2, n1)
    angle_t = np.linspace(+3 * np.pi / 2, +4 * np.pi / 2, n2)

    cl = BoundaryCurve(np.cos(angle_l), np.sin(angle_l))
    cr = BoundaryCurve(np.cos(angle_r), np.sin(angle_r))
    ct = BoundaryCurve(np.cos(angle_t), np.sin(angle_t))
    cb = BoundaryCurve(np.cos(angle_b), np.sin(angle_b))

    blockwest = MeshBlock(
        "left",
        {
            BoundaryId.BoundaryWest: cl,
            BoundaryId.BoundaryEast: BoundaryBlock("right", BoundaryId.BoundaryWest, n1),
            BoundaryId.BoundaryNorth: BoundaryBlock("top", BoundaryId.BoundaryWest, n2),
            BoundaryId.BoundarySouth: BoundaryBlock(
                "bottom", BoundaryId.BoundaryWest, n2
            ),
        },
    )
    blockeast = MeshBlock(
        "right",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("left", BoundaryId.BoundaryEast, n1),
            BoundaryId.BoundaryEast: cr,
            BoundaryId.BoundaryNorth: BoundaryBlock("top", BoundaryId.BoundaryEast, n2),
            BoundaryId.BoundarySouth: BoundaryBlock(
                "bottom", BoundaryId.BoundaryEast, n2
            ),
        },
    )
    blocknorth = MeshBlock(
        "top",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("left", BoundaryId.BoundaryNorth, n1),
            BoundaryId.BoundaryEast: BoundaryBlock("right", BoundaryId.BoundaryNorth, n1),
            BoundaryId.BoundaryNorth: ct,
            BoundaryId.BoundarySouth: BoundaryBlock(
                "bottom", BoundaryId.BoundaryNorth, n2
            ),
        },
    )
    blocksouth = MeshBlock(
        "bottom",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("left", BoundaryId.BoundarySouth, n1),
            BoundaryId.BoundaryEast: BoundaryBlock("right", BoundaryId.BoundarySouth, n1),
            BoundaryId.BoundaryNorth: BoundaryBlock("top", BoundaryId.BoundarySouth, n2),
            BoundaryId.BoundarySouth: cb,
        },
    )
    t0 = perf_counter()
    m, _, _ = create_elliptical_mesh(
        [blockwest, blockeast, blocknorth, blocksouth],
        verbose=False,
        solver_cfg=SolverConfig(smoother_rounds=0, max_iterations=64),
    )
    t1 = perf_counter()
    print(f"Meshed in {t1 - t0:g} seconds.")
    return m


# Now let's show it!

plot_mesh(four_wierdly_connected_ones(2, 2))

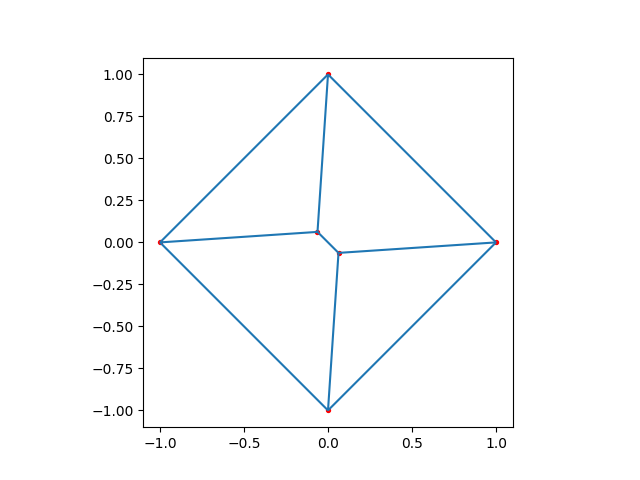
Meshed in 6.6404e-05 seconds.

plot_mesh(four_wierdly_connected_ones(10, 10))

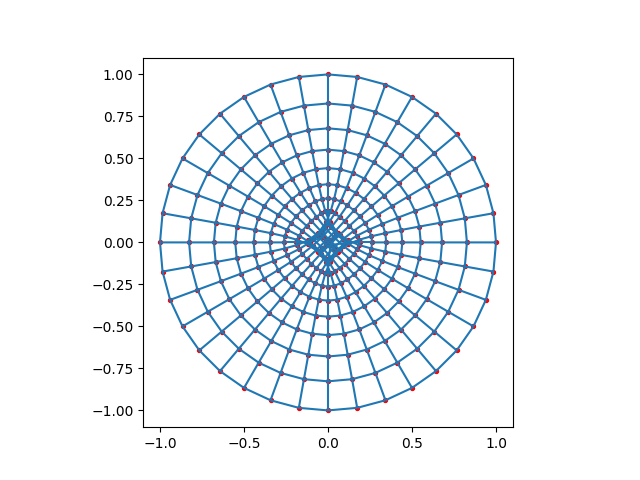
Meshed in 0.000726724 seconds.

plot_mesh(four_wierdly_connected_ones(50, 50))

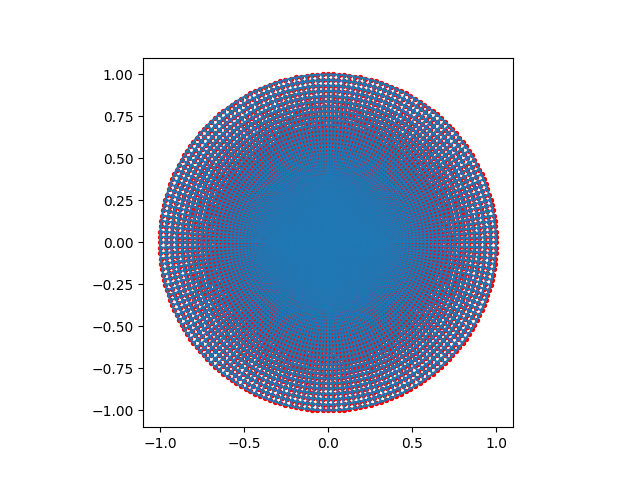
Meshed in 0.134927 seconds.

Doing it Right

Probably the best way to mesh the circle is using five blocks, so that a quarter of the boundary is take care of by one block each, then they’re all connected together using a central block with no numerical boundaries.

def as_god_intended(n1: int, n2: int, n3: int) -> Mesh2D:
    """Mesh the circle the way God intended."""
    angle_l = np.linspace(+0 * np.pi / 2, +1 * np.pi / 2, n1)
    angle_b = np.linspace(+1 * np.pi / 2, +2 * np.pi / 2, n2)
    angle_r = np.linspace(+2 * np.pi / 2, +3 * np.pi / 2, n1)
    angle_t = np.linspace(+3 * np.pi / 2, +4 * np.pi / 2, n2)

    cl = BoundaryCurve(np.cos(angle_l), np.sin(angle_l))
    cr = BoundaryCurve(np.cos(angle_r), np.sin(angle_r))
    ct = BoundaryCurve(np.cos(angle_t), np.sin(angle_t))
    cb = BoundaryCurve(np.cos(angle_b), np.sin(angle_b))

    blockwest = MeshBlock(
        "left",
        {
            BoundaryId.BoundaryWest: cl,
            BoundaryId.BoundaryEast: BoundaryBlock("center", BoundaryId.BoundaryWest, n1),
            BoundaryId.BoundaryNorth: BoundaryBlock("top", BoundaryId.BoundaryWest, n3),
            BoundaryId.BoundarySouth: BoundaryBlock(
                "bottom", BoundaryId.BoundaryWest, n3
            ),
        },
    )
    blockeast = MeshBlock(
        "right",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("center", BoundaryId.BoundaryEast, n1),
            BoundaryId.BoundaryEast: cr,
            BoundaryId.BoundaryNorth: BoundaryBlock("top", BoundaryId.BoundaryEast, n3),
            BoundaryId.BoundarySouth: BoundaryBlock(
                "bottom", BoundaryId.BoundaryEast, n3
            ),
        },
    )
    blocknorth = MeshBlock(
        "top",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("left", BoundaryId.BoundaryNorth, n3),
            BoundaryId.BoundaryEast: BoundaryBlock("right", BoundaryId.BoundaryNorth, n3),
            BoundaryId.BoundaryNorth: ct,
            BoundaryId.BoundarySouth: BoundaryBlock(
                "center", BoundaryId.BoundaryNorth, n2
            ),
        },
    )
    blocksouth = MeshBlock(
        "bottom",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("left", BoundaryId.BoundarySouth, n3),
            BoundaryId.BoundaryEast: BoundaryBlock("right", BoundaryId.BoundarySouth, n3),
            BoundaryId.BoundaryNorth: BoundaryBlock(
                "center", BoundaryId.BoundarySouth, n2
            ),
            BoundaryId.BoundarySouth: cb,
        },
    )
    blockmiddle = MeshBlock(
        "center",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("left", BoundaryId.BoundaryEast, n1),
            BoundaryId.BoundaryEast: BoundaryBlock("right", BoundaryId.BoundaryWest, n1),
            BoundaryId.BoundaryNorth: BoundaryBlock("top", BoundaryId.BoundarySouth, n2),
            BoundaryId.BoundarySouth: BoundaryBlock(
                "bottom", BoundaryId.BoundaryNorth, n2
            ),
        },
    )

    t0 = perf_counter()
    m, _, _ = create_elliptical_mesh(
        [blockwest, blockeast, blocknorth, blocksouth, blockmiddle],
        verbose=False,
        solver_cfg=SolverConfig(
            smoother_rounds=0, max_iterations=64, tolerance=5e-6, force_direct=False
        ),
    )
    t1 = perf_counter()
    print(f"Meshed in {t1 - t0:g} seconds.")
    return m

plot_mesh(as_god_intended(2, 2, 2))

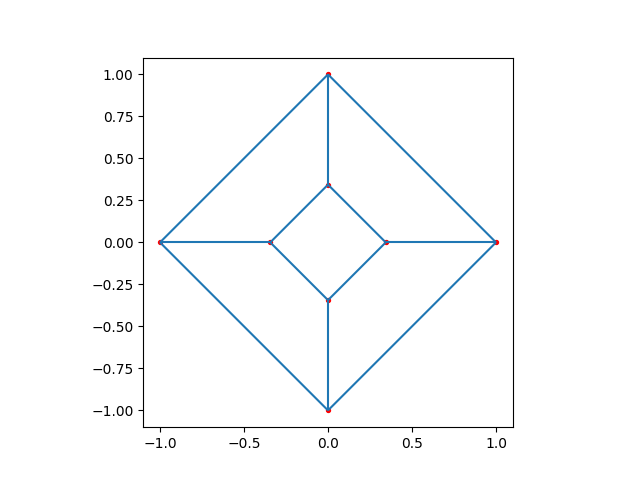
Meshed in 8.061e-05 seconds.

plot_mesh(as_god_intended(5, 5, 5))

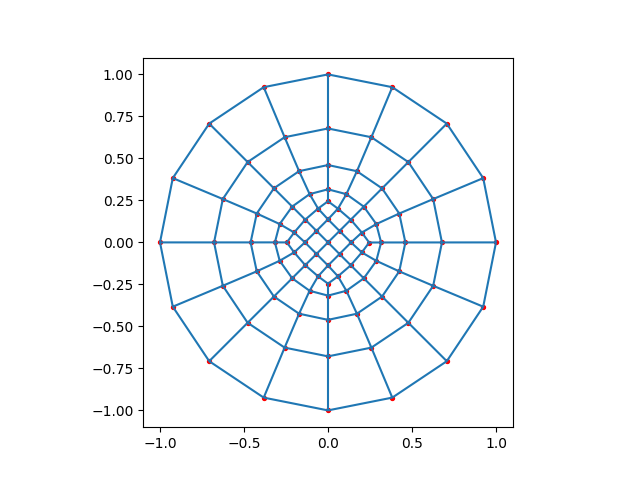
Meshed in 0.000360712 seconds.

plot_mesh(as_god_intended(25, 25, 25))

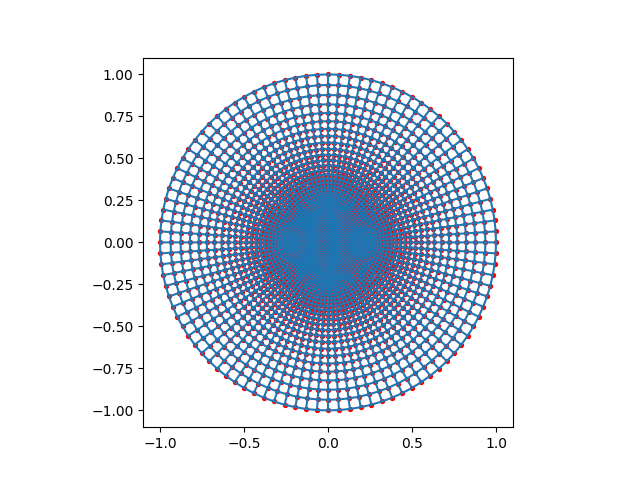
Meshed in 0.0188475 seconds.

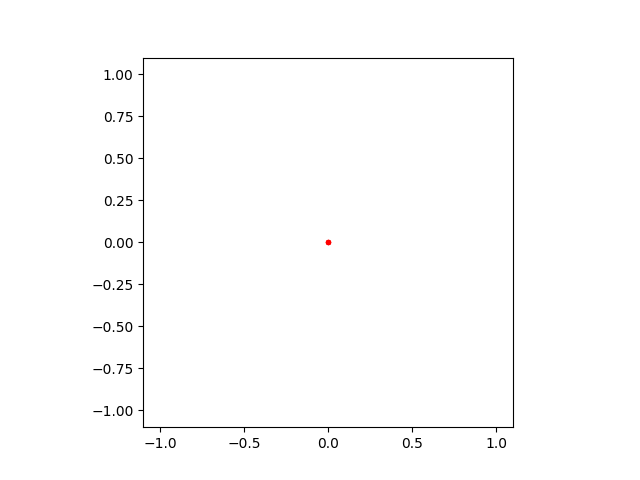
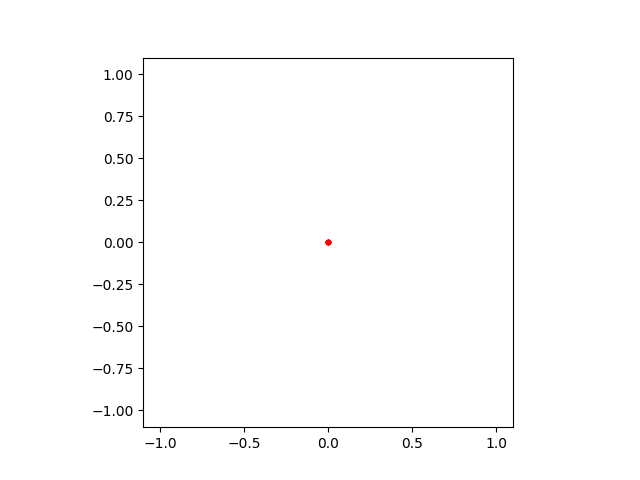
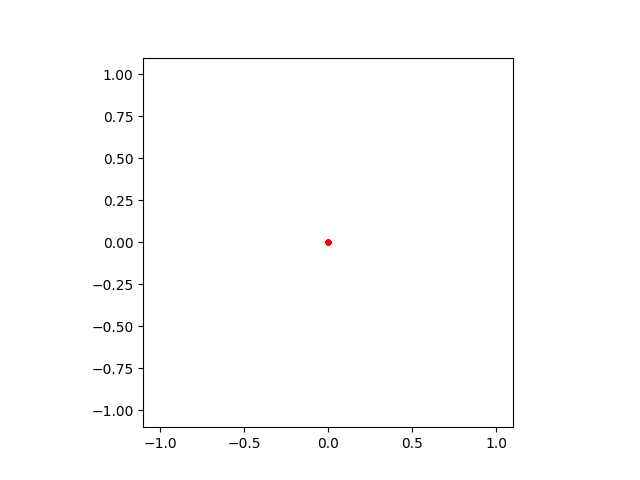
No Boundaries

If you decide to define a mesh which has no numerical boundaries, it is technically possible, however, the solver will just place all points in the origin, though the topology will still remain correct.

def ungodly(n1: int, n2: int) -> Mesh2D:
    """Mesh with no hard boundaries."""
    blockmiddle = MeshBlock(
        "center",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("center", BoundaryId.BoundaryEast, n1),
            BoundaryId.BoundaryEast: BoundaryBlock("center", BoundaryId.BoundaryWest, n1),
            BoundaryId.BoundaryNorth: BoundaryBlock(
                "center", BoundaryId.BoundarySouth, n2
            ),
            BoundaryId.BoundarySouth: BoundaryBlock(
                "center", BoundaryId.BoundaryNorth, n2
            ),
        },
    )

    t0 = perf_counter()
    m, _, _ = create_elliptical_mesh(
        [blockmiddle],
        verbose=False,
        solver_cfg=SolverConfig(smoother_rounds=0, max_iterations=64),
    )
    t1 = perf_counter()
    print(f"Meshed in {t1 - t0:g} seconds.")
    return m

plot_mesh(ungodly(2, 2))

Meshed in 2.8743e-05 seconds.

plot_mesh(ungodly(5, 5))

Meshed in 4.2429e-05 seconds.

plot_mesh(ungodly(25, 25))

Meshed in 0.000329073 seconds.

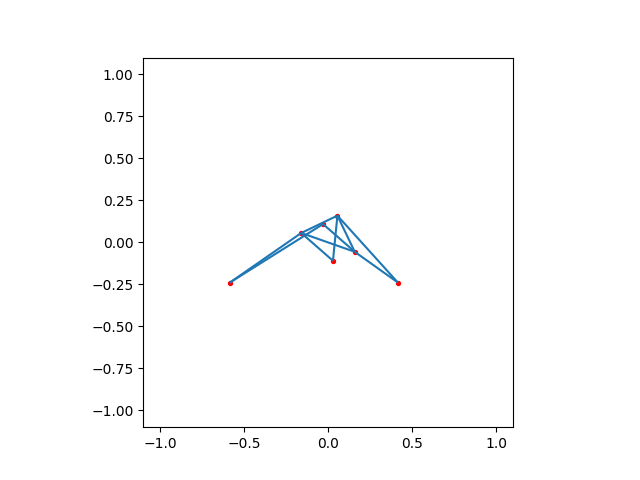
Mixing Up Boundaries

Once, again, mixing up boundaries will inevitably result in a self-overlapping mesh. This example here does so with four different blocks.

def four_weirder(n: int) -> Mesh2D:
    """Outer boundary's correct, but the rest is not."""
    angle_l = np.linspace(+0 * np.pi / 2, +1 * np.pi / 2, n)
    angle_b = np.linspace(+1 * np.pi / 2, +2 * np.pi / 2, n)
    angle_r = np.linspace(+2 * np.pi / 2, +3 * np.pi / 2, n)
    angle_t = np.linspace(+3 * np.pi / 2, +4 * np.pi / 2, n)

    cl = BoundaryCurve(np.cos(angle_l), np.sin(angle_l))
    cr = BoundaryCurve(np.cos(angle_r), np.sin(angle_r))
    ct = BoundaryCurve(np.cos(angle_t), np.sin(angle_t))
    cb = BoundaryCurve(np.cos(angle_b), np.sin(angle_b))

    blockwest = MeshBlock(
        "left",
        {
            BoundaryId.BoundaryWest: cl,
            BoundaryId.BoundaryEast: BoundaryBlock("bottom", BoundaryId.BoundaryWest),
            BoundaryId.BoundaryNorth: BoundaryBlock("top", BoundaryId.BoundarySouth),
            BoundaryId.BoundarySouth: BoundaryBlock("right", BoundaryId.BoundaryNorth),
        },
    )
    blockeast = MeshBlock(
        "right",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("top", BoundaryId.BoundaryEast),
            BoundaryId.BoundaryEast: cr,
            BoundaryId.BoundaryNorth: BoundaryBlock("left", BoundaryId.BoundarySouth),
            BoundaryId.BoundarySouth: BoundaryBlock("bottom", BoundaryId.BoundaryNorth),
        },
    )
    blocknorth = MeshBlock(
        "top",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("bottom", BoundaryId.BoundaryEast),
            BoundaryId.BoundaryEast: BoundaryBlock("right", BoundaryId.BoundaryWest),
            BoundaryId.BoundaryNorth: ct,
            BoundaryId.BoundarySouth: BoundaryBlock("left", BoundaryId.BoundaryNorth),
        },
    )
    blocksouth = MeshBlock(
        "bottom",
        {
            BoundaryId.BoundaryWest: BoundaryBlock("left", BoundaryId.BoundaryEast),
            BoundaryId.BoundaryEast: BoundaryBlock("top", BoundaryId.BoundaryWest),
            BoundaryId.BoundaryNorth: BoundaryBlock("right", BoundaryId.BoundarySouth),
            BoundaryId.BoundarySouth: cb,
        },
    )

    t0 = perf_counter()
    m, _, _ = create_elliptical_mesh(
        [blockwest, blockeast, blocknorth, blocksouth],
        verbose=False,
        solver_cfg=SolverConfig(smoother_rounds=0, max_iterations=64),
    )
    t1 = perf_counter()
    print(f"Meshed in {t1 - t0:g} seconds.")
    return m

plot_mesh(four_weirder(2))

Meshed in 9.4667e-05 seconds.

plot_mesh(four_weirder(10))

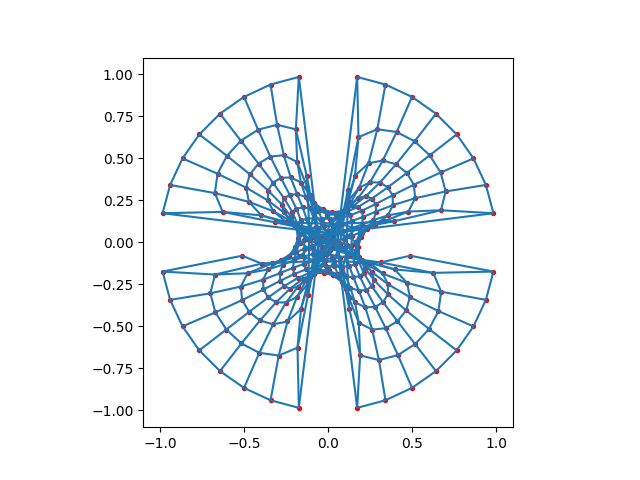
Meshed in 0.000762533 seconds.

plot_mesh(four_weirder(50))

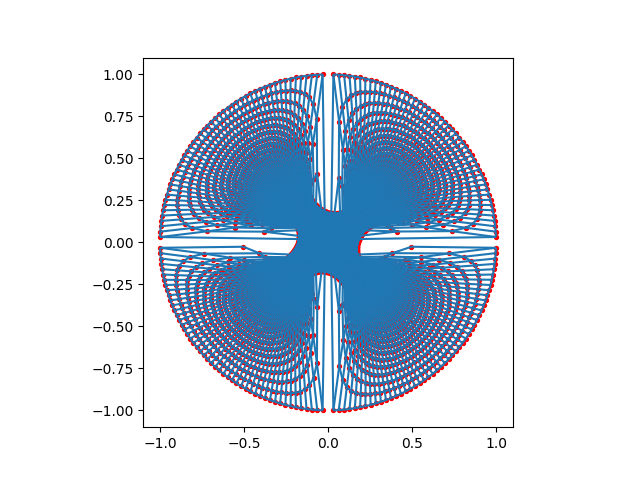
Meshed in 0.0690637 seconds.