Note
Go to the end to download the full example code.
Approximating Error from Projections with Advection-Diffusion#
Using exact solution as a refinement criterion is a luxury that’s not often availabel for real problems. As such, process in the example Post-Solver Combined hp-refinement with Direct Poisson may not be possible to replicate.
As such, this example shows how error can be estimated using projection to a finer mesh. This means that a problem is solved twice, with same topology, but different element orders. The finer one is then taken as being much closer to the real solution and thus used to compute an error estimate.
from functools import partial
import numpy as np
import numpy.typing as npt
import pyvista as pv
import rmsh
from matplotlib import pyplot as plt
from matplotlib.collections import PolyCollection
from mfv2d import (
ErrorEstimateExplicit,
KFormSystem,
KFormUnknown,
Mesh,
RefinementLimitElementCount,
RefinementSettings,
SystemSettings,
UnknownFormOrder,
mesh_create,
solve_system_2d,
system_as_string,
)
Problem Description#
The model problem that is to be solved here is the linear advection diffusion equation on a deformed square domain, with the solution given by equation (2), where the function \(s\) is specified by equation (1). The advection vector field is given by
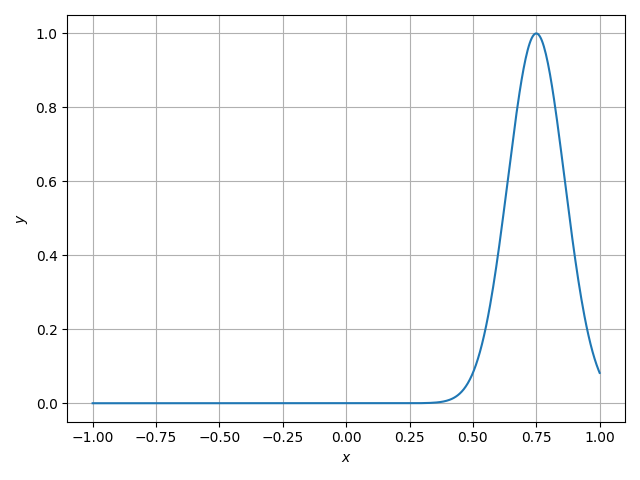
The cross section of the solution can be seen in the plot bellow.
R = 40.0
def s(t: npt.NDArray[np.float64], r: float, t0: float) -> npt.NDArray[np.floating]:
"""Compute source term."""
return np.exp(-r * (t - t0) ** 2)
def dsdt(t: npt.NDArray[np.float64], r: float, t0: float) -> npt.NDArray[np.floating]:
"""Compute derivative source term."""
return -2 * r * (t - t0) * np.exp(-r * (t - t0) ** 2)
def d2sdt2(t: npt.NDArray[np.float64], r: float, t0: float) -> npt.NDArray[np.floating]:
"""Compute second derivative source term."""
return 2 * r * (2 * r * (t - t0) ** 2 - 1) * np.exp(-r * (t - t0) ** 2)
def u_exact(x: npt.NDArray[np.float64], y: npt.NDArray[np.float64]):
"""Exact solution."""
return s(x, R, 0.75) * s(y, R, 0.75)
def q_exact(x: npt.NDArray[np.float64], y: npt.NDArray[np.float64]):
"""Exact gradient of solution."""
return np.stack(
(
dsdt(x, R, 0.75) * s(y, R, 0.75),
s(x, R, 0.75) * dsdt(y, R, 0.75),
),
axis=-1,
)
def adv_field(x: npt.NDArray[np.float64], y: npt.NDArray[np.float64]):
"""Advection field."""
return np.stack(
(3 * x + y, x**2 - y**3),
axis=-1,
)
def source_exact(x: npt.NDArray[np.float64], y: npt.NDArray[np.float64]):
"""Exact heat flux divergence."""
return (
s(x, R, 0.75) * d2sdt2(y, R, 0.75) + d2sdt2(x, R, 0.75) * s(y, R, 0.75)
) + np.sum(adv_field(x, y) * q_exact(x, y), axis=-1)
fig, ax = plt.subplots()
xplt = np.linspace(-1, +1, 501, dtype=np.float64)
ax.plot(xplt, s(xplt, R, 0.75))
ax.grid()
ax.set(xlabel="$x$", ylabel="$y$")
fig.tight_layout()
plt.show()
System Setup#
System setup for this is exactly the same as it was for other examples, with the system and boundary conditions specified. Since the problem is written in the mixed formulation, Dirichlet boundary conditions are weakly imposed.
u = KFormUnknown("u", UnknownFormOrder.FORM_ORDER_2)
v = u.weight
q = KFormUnknown("q", UnknownFormOrder.FORM_ORDER_1)
p = q.weight
system = KFormSystem(
p @ q + p.derivative @ u == p ^ u_exact,
v @ q.derivative - (adv_field * v @ q) == v @ source_exact,
)
print(system_as_string(system))
[M(1) | (E(2, 1))^T M(2)] [q(1)] [+ B<q, u_exact> ] [0 | 0] [q(1)]
[+ (M(2) E(2, 1)) + (-1.0 (P(1, 2, adv_field))^T) | 0 ] [u(2)] = [+ E<u, source_exact>] + [0 | 0] [u(2)]
Making the Mesh#
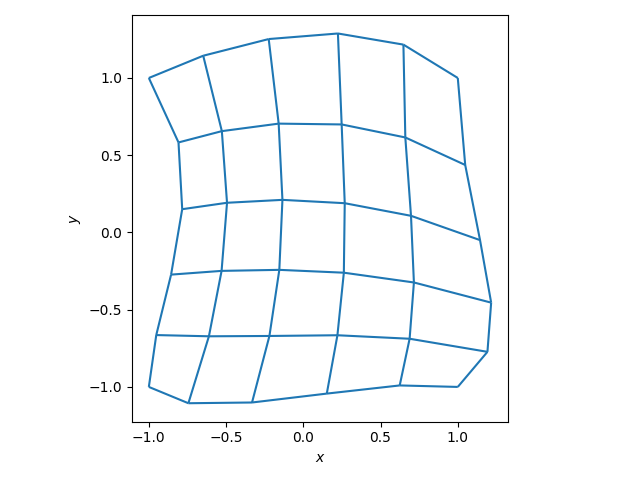
The mesh is a deformed square, as mentioned before. Its corners match the unit square, but the sides are curved. There are five elements in every direction.
Initial mesh can be seen bellow.
N = 6
n1 = N
n2 = N
m, rx, ry = rmsh.create_elliptical_mesh(
rmsh.MeshBlock(
None,
rmsh.BoundaryCurve.from_knots(
n1, (-1, -1), (-0.75, -1.3), (+0.5, -0.9), (+1, -1)
), # bottom
rmsh.BoundaryCurve.from_knots(
n2, (+1, -1), (+1.5, -0.7), (+1, 0.0), (+1, +1)
), # right
rmsh.BoundaryCurve.from_knots(
n1, (+1, +1), (0.5, 1.5), (-0.5, 1.25), (-1, +1)
), # top
rmsh.BoundaryCurve.from_knots(
n2, (-1, +1), (-0.5, 0.33), (-1, -0.5), (-1, -1)
), # left
)
)
assert rx < 1e-6 and ry < 1e-6
fig, ax = plt.subplots()
m.plot(ax)
ax.autoscale()
ax.set(xlabel="$x$", ylabel="$y$", aspect="equal")
fig.tight_layout()
plt.show()
Initialize the Mesh#
With geometry created, it is converted into suitable form to use with mfv2d.
Also a convinience function plot_mesh_comparisons is defined here, to allow for
simple comparison of meshes.
PSTART = 1 # Test polynomial order
mesh_initial = mesh_create(
PSTART, np.stack((m.pos_x, m.pos_y), axis=-1), m.lines + 1, m.surfaces
)
def plot_mesh_comparisons(*meshes: tuple[str, Mesh]) -> None:
"""Plot one or more meshes with given titles."""
fig, axes = plt.subplots(len(meshes), 1, figsize=(5, 7 * len(meshes)))
for ax, (title, mesh) in zip(axes, meshes, strict=True):
vertices = [mesh.get_leaf_corners(idx) for idx in mesh.get_leaf_indices()]
ax.add_collection(PolyCollection(vertices, facecolors="none", antialiased=True))
for idx, quad in zip(mesh.get_leaf_indices(), vertices):
ax.text(
*np.mean(quad, axis=0),
f"{np.linalg.norm(mesh.get_leaf_orders(idx)) / np.sqrt(2):.3g}",
ha="center",
va="center",
color="red",
fontsize=6,
)
ax.autoscale()
ax.set(aspect="equal", title=title)
fig.tight_layout()
plt.show()
Refinement Settings#
For error refinement, the main difference occurs in how the error calculation
function is written. Instead of using the exact solution, the fine_solution
keyword argument is taken, interpolated on the integration points’ positions
x and y, which is then used to estimate error.
def reconstruct_fine(
x: npt.NDArray[np.float64],
y: npt.NDArray[np.float64],
*,
fine_solution: pv.UnstructuredGrid,
form: KFormUnknown,
) -> npt.NDArray[np.float64]:
"""Compute the reconstruction of the fine solutions."""
zeros = 0 * x + 0 * y
points = np.stack((x + 0 * y, 0 * x + y, zeros), axis=-1).reshape((-1, 3))
pts = pv.PolyData(points)
interpolated = pts.sample(fine_solution)
resulting_data = interpolated.point_data[form.label]
return np.reshape(resulting_data, zeros.shape)
N_ROUNDS = 12
system_settings = SystemSettings(system=system)
Evaluating a Refinement Strategy#
Evaluation of refinement strategies is similar to how it was in
Post-Solver Combined hp-refinement with Direct Poisson,
with the difference being that the problem is first solved on a mesh
where all elements are have all elements with orders increased by dp,
which is then passed to the error estimation function as fine_solution.
RUN_COUNT = 0
def run_refinement_strategy(dp: int, h_ratio: float, max_elements: int, mesh: Mesh):
"""Compute errors and resulting mesh for a refinement strategy."""
global RUN_COUNT
errors_local: list[tuple[int, float]] = list()
new_mesh = mesh.copy()
# new_mesh.uniform_p_change(+dp, +dp)
plotter = pv.Plotter(off_screen=True, window_size=(1600, 900), shape=(1, 2))
plotter.open_gif(f"direct-poisson-post-hp-{RUN_COUNT:d}.gif", fps=1)
RUN_COUNT += 1
for i_round in range(N_ROUNDS):
mesh = new_mesh
# Obtain the finer solution
mesh.uniform_p_change(+dp, +dp)
fine_solutions, statistics, _ = solve_system_2d(
mesh,
system_settings=system_settings,
refinement_settings=None,
recon_order=15,
)
# Change mesh order back
mesh.uniform_p_change(-dp, -dp)
refinement_settings = RefinementSettings(
# Specifying how the error is estimated
error_estimate=ErrorEstimateExplicit(
# Required by the error function
target_form=u,
# The error (estimation) function
solution_estimate=partial(
reconstruct_fine, fine_solution=fine_solutions[-1], form=u
),
),
# H-refinement when ratio of h-cost and error less than this
h_refinement_ratio=h_ratio,
# When to stop refining
refinement_limit=RefinementLimitElementCount(1.0, max_elements),
# Print error distribution to terminal
report_error_distribution=True,
# Print element order distribution to terminal
report_order_distribution=True,
)
solutions, statistics, new_mesh = solve_system_2d(
mesh,
system_settings=system_settings,
refinement_settings=refinement_settings,
recon_order=15,
)
solution = solutions[-1]
# solution = fine_solutions[-1]
u_computed = solution.point_data[u.label]
u_real = u_exact(solution.points[:, 0], solution.points[:, 1])
l2_err2 = (u_real - u_computed) ** 2
solution.point_data["l2_error2"] = l2_err2
errors_local.append(
(
statistics.n_total_dofs,
np.sqrt(solution.integrate_data().point_data["l2_error2"][0]),
)
)
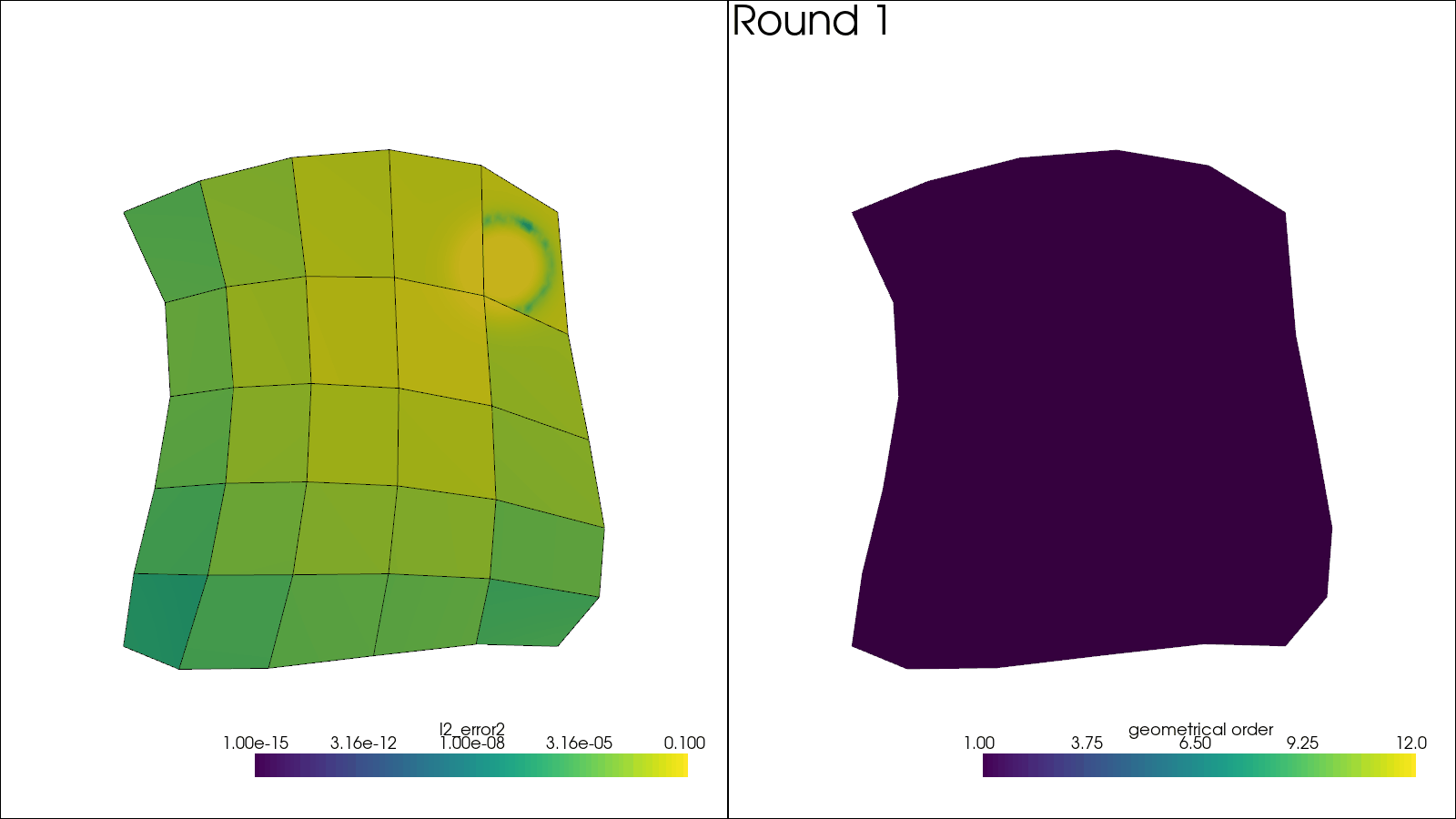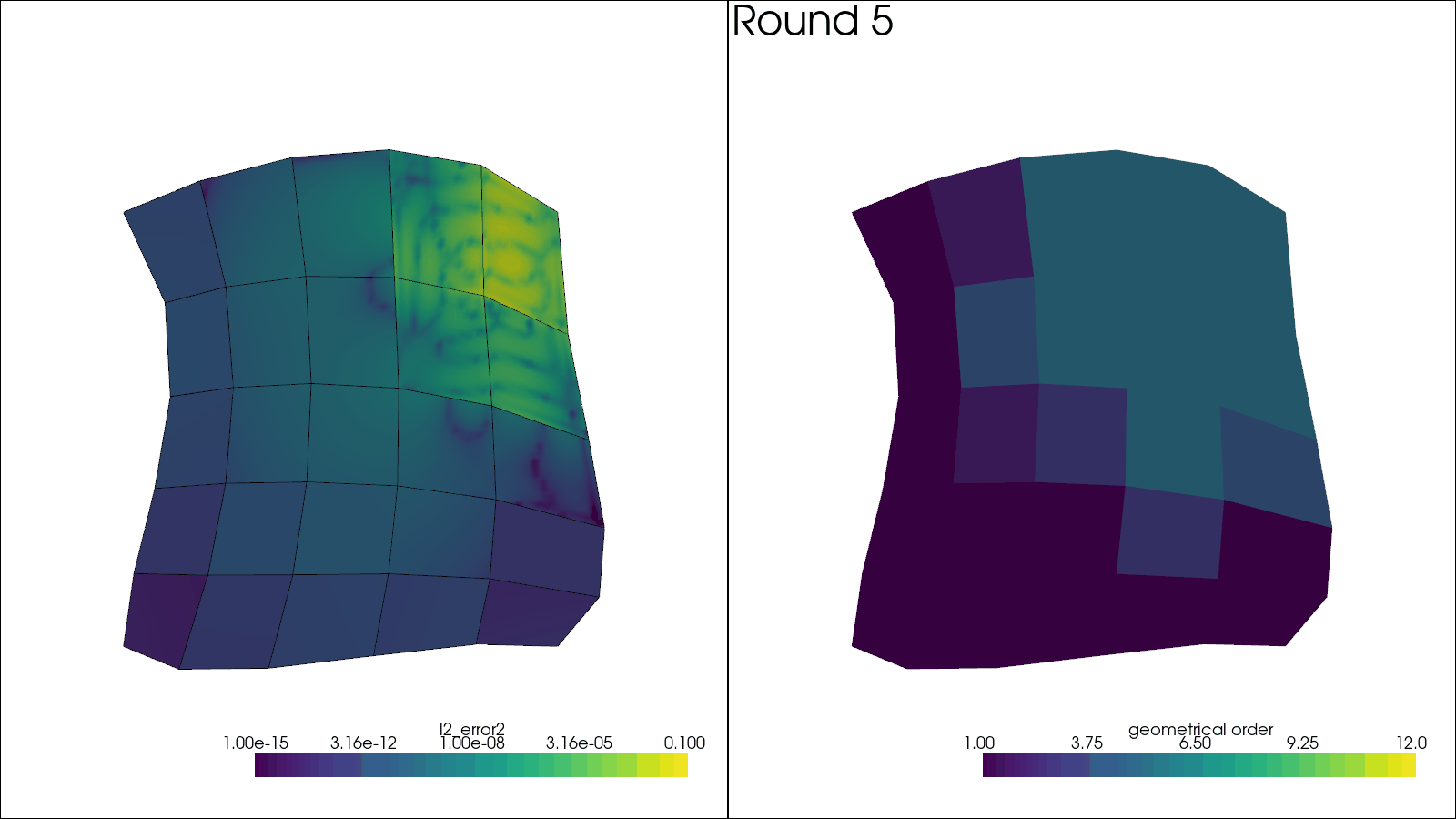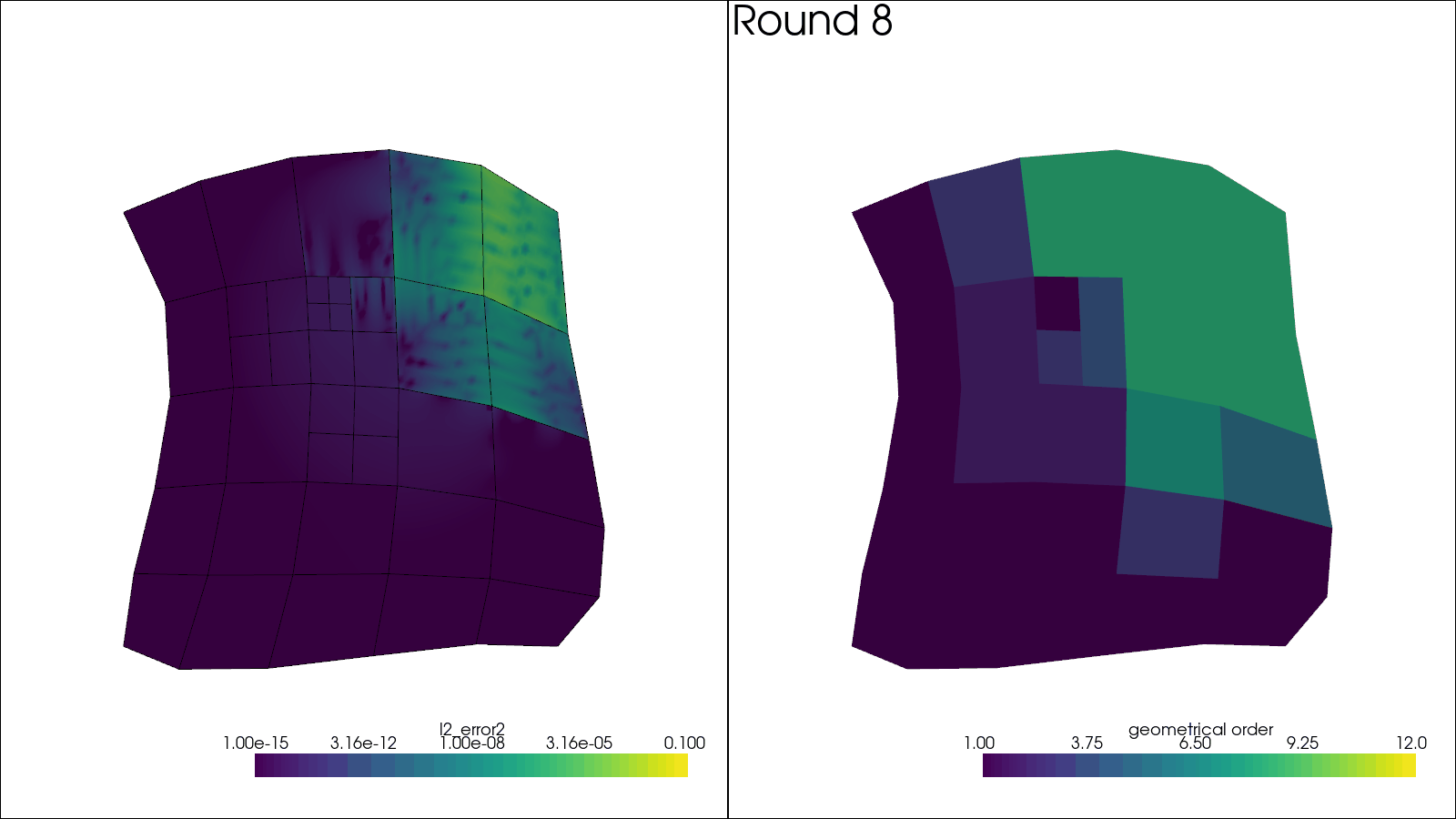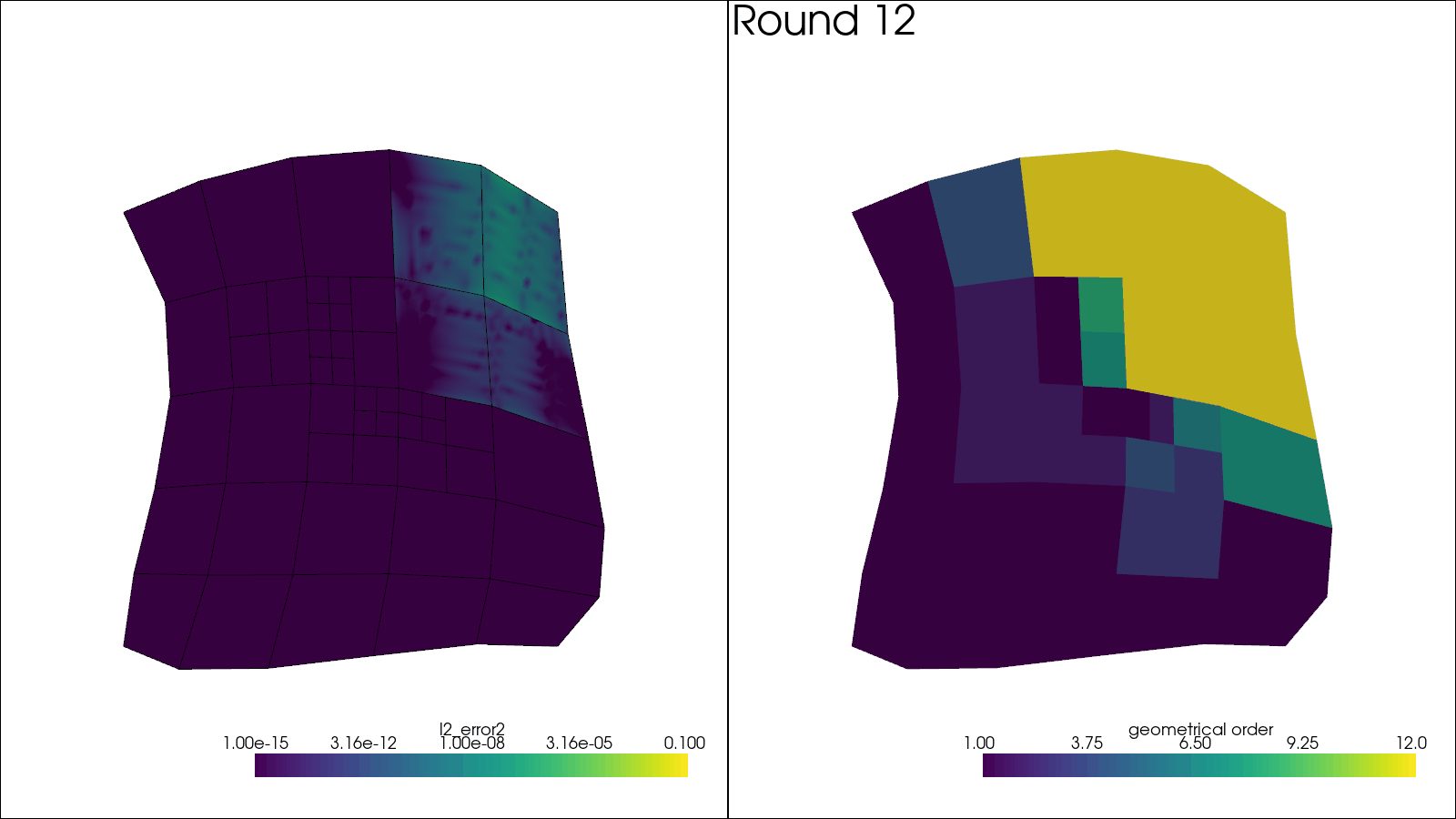
# Plotting code here
plotter.subplot(0, 0)
plotter.add_mesh(
solution,
scalars="l2_error2",
log_scale=True,
label="$L^2$ error",
clim=(1e-15, 1e-1),
name="solution",
)
plotter.add_mesh(
solution.extract_all_edges(), scalars=None, color="black", name="boundaries"
)
plotter.view_xy()
plotter.subplot(0, 1)
sol = solution.copy()
sol.cell_data["geometrical order"] = np.linalg.norm(
[mesh.get_leaf_orders(ie) for ie in mesh.get_leaf_indices()], axis=-1
) / np.sqrt(2)
plotter.add_mesh(sol, scalars="geometrical order", name="orders", clim=(1, 12))
plotter.add_text(f"Round {i_round + 1:d}", name="title")
plotter.view_xy()
plotter.write_frame()
plotter.close()
return errors_local, mesh
Baseline Data#
Again, uniform p-refinement is used as baseline to show benefits of local hp-refinement.
errors_uniform: list[tuple[int, float]] = list()
uniform_mesh = mesh_initial.copy()
for pval in range(PSTART, 9):
solutions, statistics, _ = solve_system_2d(
uniform_mesh,
system_settings=system_settings,
refinement_settings=None,
recon_order=15,
)
solution = solutions[-1]
u_computed = solution.point_data[u.label]
u_real = u_exact(solution.points[:, 0], solution.points[:, 1])
l2_err2 = (u_real - u_computed) ** 2
solution.point_data["l2_error2"] = l2_err2
errors_uniform.append(
(
statistics.n_total_dofs,
np.sqrt(solution.integrate_data().point_data["l2_error2"][0]),
)
)
uniform_mesh.uniform_p_change(1, 1) # Up the mesh orders
Running hp-Refinement#
For all hp-runs, the values of 0.1 and 10 were taken as values of
h-refinement ratio and element limit count. The things that were
changed was the polynomial order difference dp.
\(dp = 1\)#
BASE_H_RATIO = 0.05
BASE_ELEMENT_LIMIT = 10
errors_local_1, local_mesh_1 = run_refinement_strategy(
1, BASE_H_RATIO, BASE_ELEMENT_LIMIT, mesh_initial
)
def err_name(dp: int) -> str:
"""Format name for error plots."""
return f"$\\Delta p ={dp:d}$"
errors_local_name_1 = err_name(1)
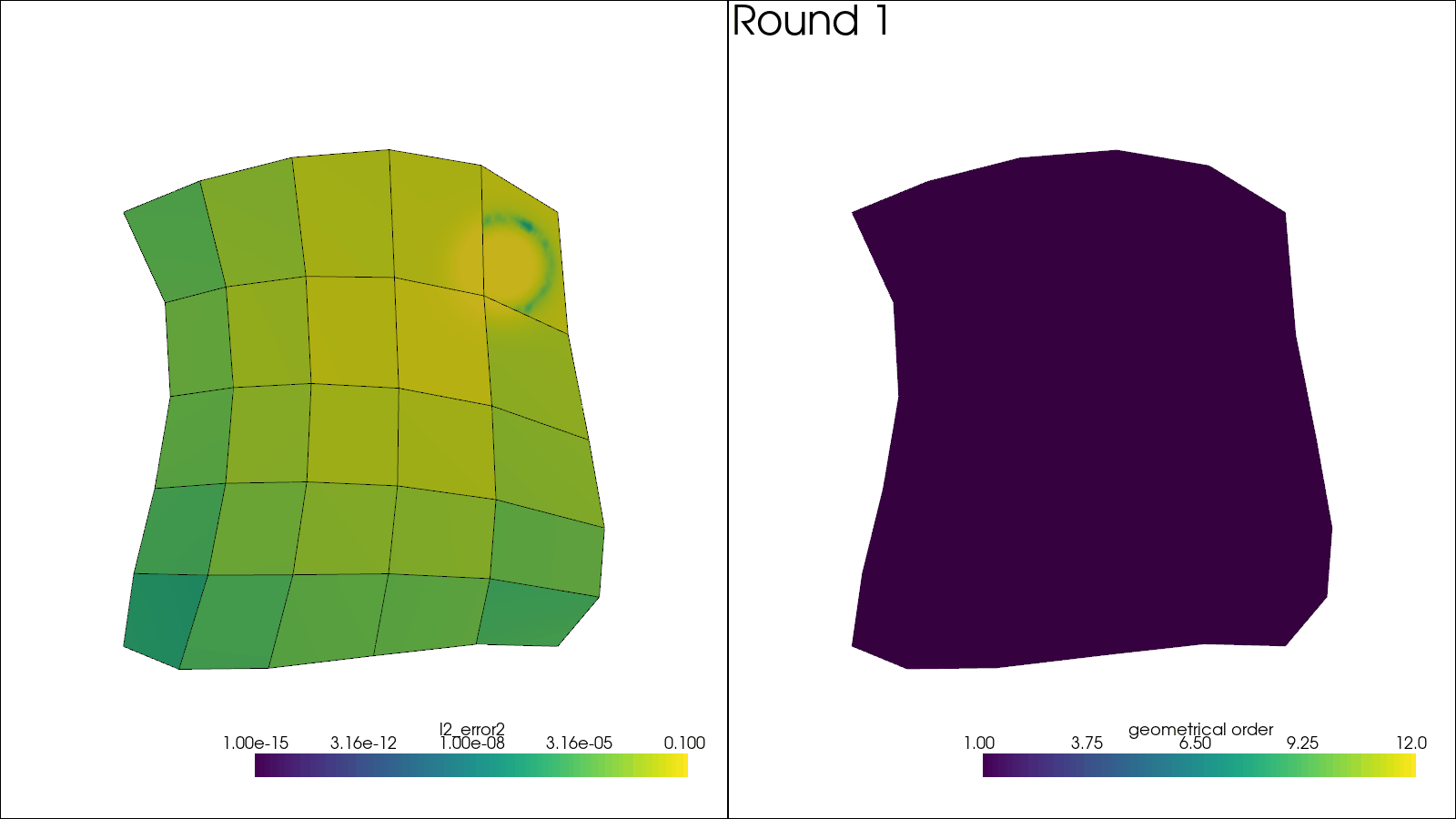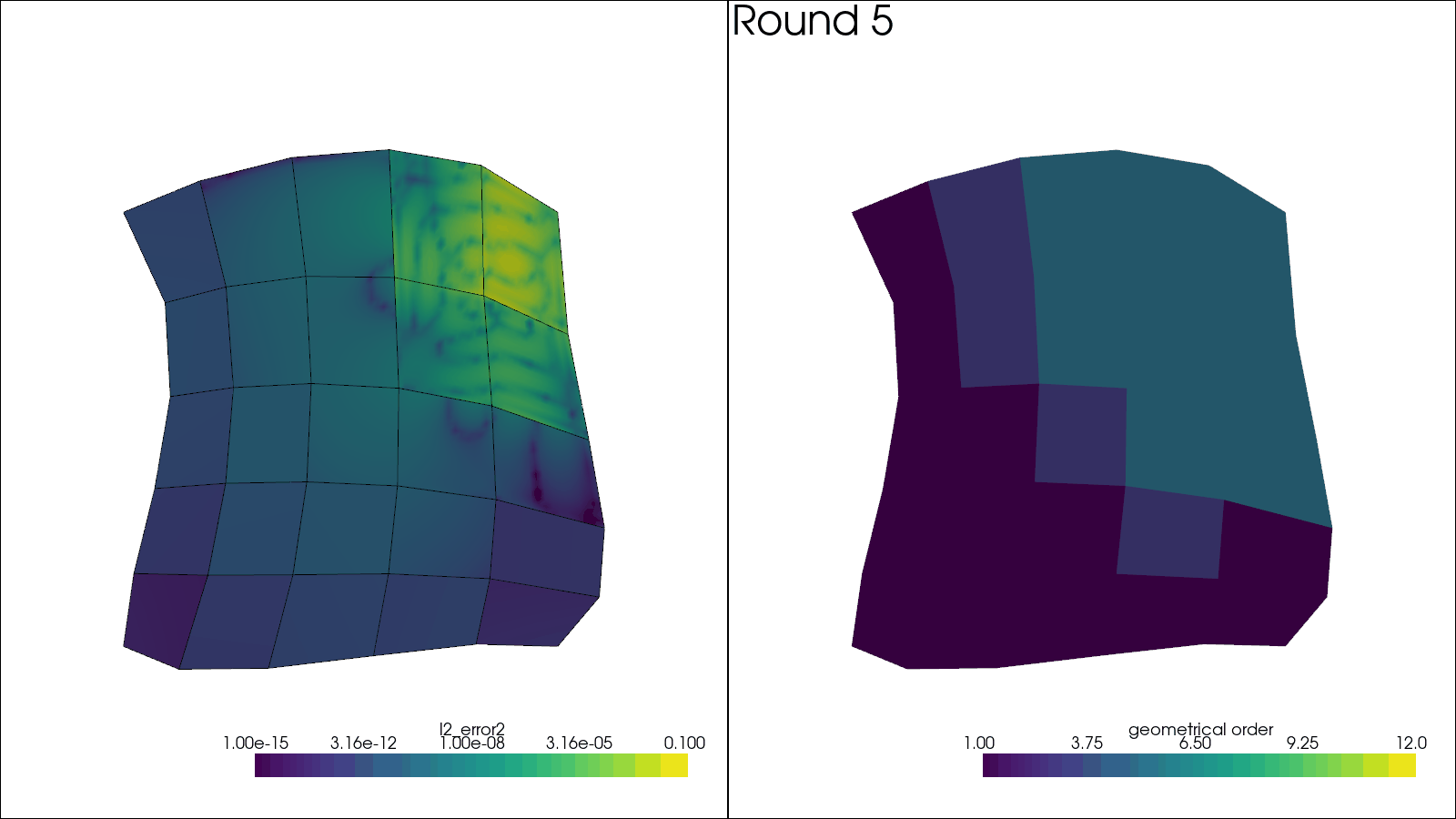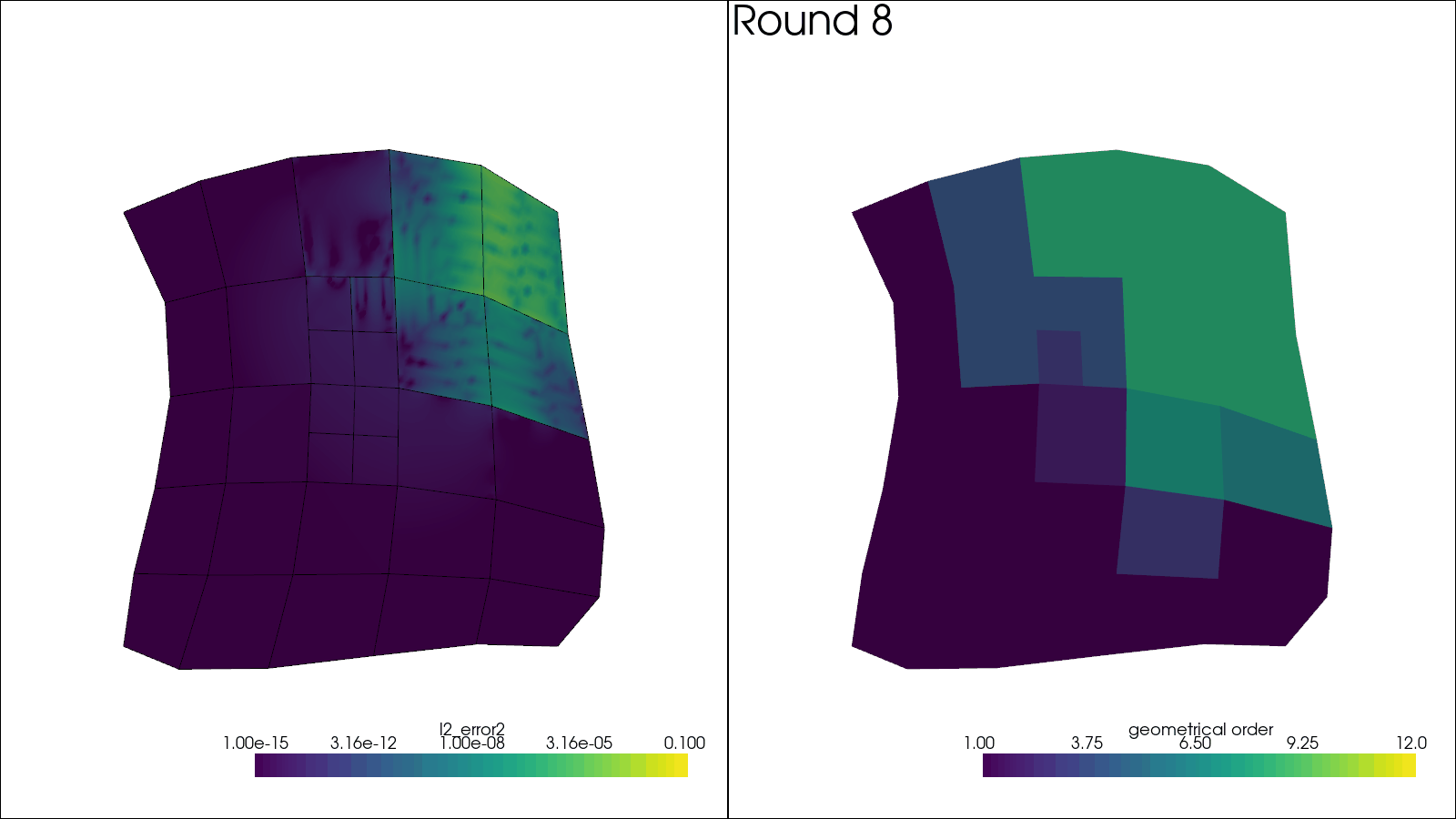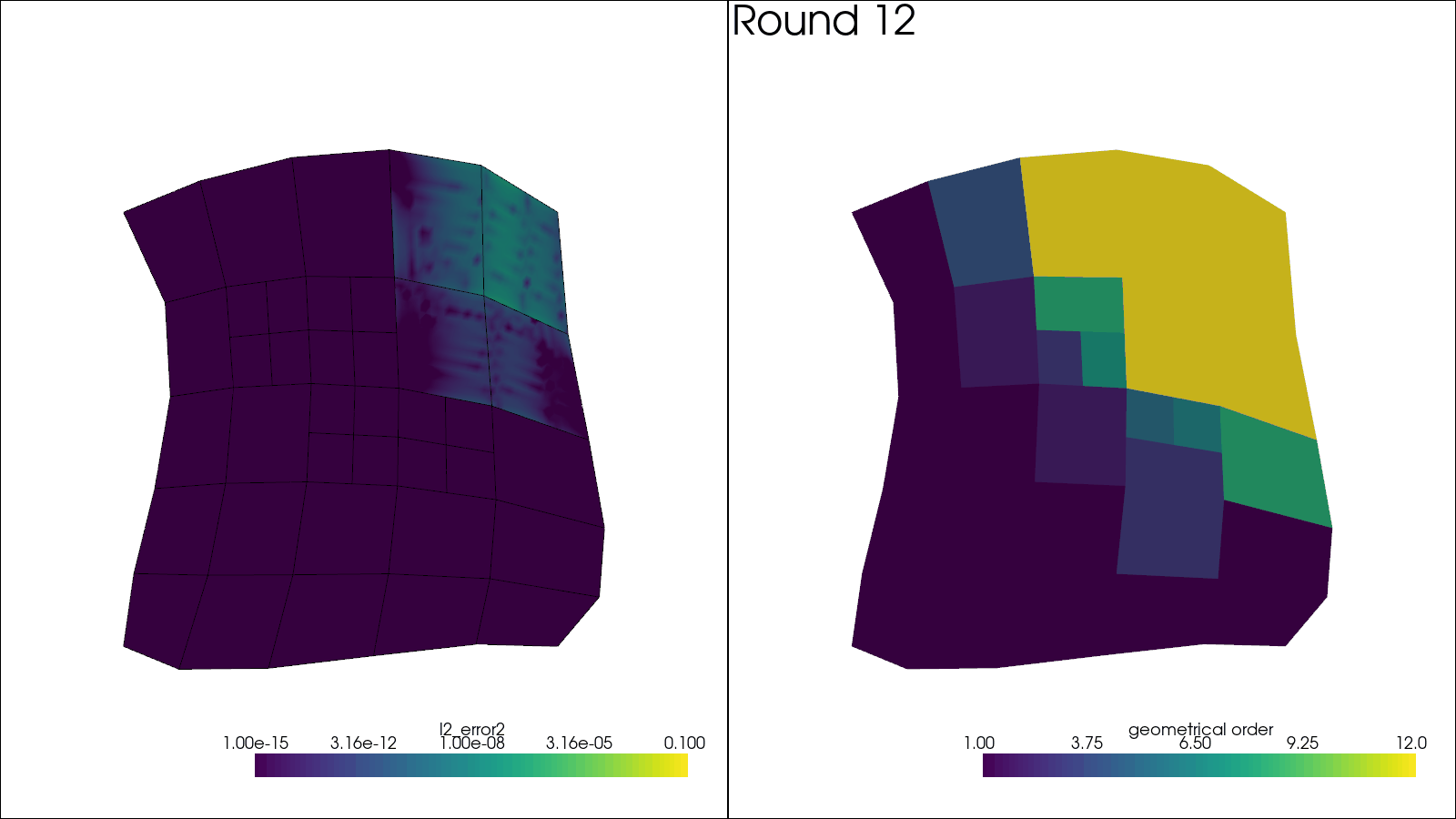
Initial mesh order distribution
============================================================
█
█
█
█
████████████████████████████████████████████████████████████
| | | | |
0.5 0.7 1.0 1.2 1.5
============================================================
Error estimate distribution
============================================================
█ █ ██ █ █
█ █ ██ █ █
█ █ █ █ █ ███ █ ███ █ █ █ █ ██ █
█ █ █ █ █ ███ █ ███ █ █ █ █ ██ █
████████████████████████████████████████████████████████████
| | | | |
10^(-7) 10^(-5.7) 10^(-4.3) 10^(-3) 10^(-1.6)
============================================================
Refined mesh order distribution
============================================================
█
█ █
█ █
█ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.2 1.5 1.7 2.0
============================================================
Initial mesh order distribution
============================================================
█
█ █
█ █
█ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.2 1.5 1.7 2.0
============================================================
Error estimate distribution
============================================================
█ █ █ █
█ █ █ █
█ █ █ █ █ ████ █ ██ ██ █ █ █ ██ █ █
█ █ █ █ █ ████ █ ██ ██ █ █ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-10) 10^(-8.2) 10^(-6.2) 10^(-4.2) 10^(-2.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.5 2.0 2.5 3.0
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.5 2.0 2.5 3.0
============================================================
Error estimate distribution
============================================================
█
█ █ █
█ █ █
█ ████ █ ██ █ █ █ █ █ █ ██ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-11) 10^(-8.9) 10^(-6.7) 10^(-4.5) 10^(-2.3)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.7 2.5 3.2 4.0
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.7 2.5 3.2 4.0
============================================================
Error estimate distribution
============================================================
█ █
█ █
█ ██ ██ ██ █ ████ █ █████ █ █ █ █ █
█ ██ ██ ██ █ ████ █ █████ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-13) 10^(-11) 10^(-8.3) 10^(-5.9) 10^(-3.4)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.9 2.9 3.9 4.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.9 2.9 3.9 4.9
============================================================
Error estimate distribution
============================================================
█ █ █ █
█ █ █ █
█ █ ██ █████ ████ █ ██ █ █ █ █ █
█ █ ██ █████ ████ █ ██ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-14) 10^(-12) 10^(-8.9) 10^(-6.2) 10^(-3.5)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.2 3.4 4.7 5.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.2 3.4 4.7 5.9
============================================================
Error estimate distribution
============================================================
█
█
█ ██ █ █ █
█ █ █ ███ ███ ██████ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-16) 10^(-14) 10^(-11) 10^(-7.5) 10^(-4.4)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.4 3.9 5.4 6.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.4 3.9 5.4 6.9
============================================================
Error estimate distribution
============================================================
█
█ █ █
█ █ █ ███
█ ██ ████ █████ █ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-18) 10^(-15) 10^(-11) 10^(-8.2) 10^(-4.9)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.6 4.4 6.1 7.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.6 4.4 6.1 7.9
============================================================
Error estimate distribution
============================================================
█ █
█ █
█ █ ██ ██
█ ██ ███ █████ █ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-19) 10^(-16) 10^(-12) 10^(-9.1) 10^(-5.7)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.9 4.9 6.9 8.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.9 4.9 6.9 8.9
============================================================
Error estimate distribution
============================================================
█
██ █
██ █
█ █ █████████████ █ █ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-21) 10^(-18) 10^(-14) 10^(-10) 10^(-6.6)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █ █
█ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.1 5.3 7.6 9.8
============================================================
Initial mesh order distribution
============================================================
█
█
█ █ █ █
█ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.1 5.3 7.6 9.8
============================================================
Error estimate distribution
============================================================
██
█ ██
█ █ ██████ █ █
█ ██ ████████ ██ █ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-23) 10^(-19) 10^(-15) 10^(-11) 10^(-7.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.3 5.8 8.3 10.8
============================================================
Initial mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.3 5.8 8.3 10.8
============================================================
Error estimate distribution
============================================================
█
██
██ █ █
█ █████████ █ █ █ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-25) 10^(-21) 10^(-17) 10^(-12) 10^(-8.3)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.6 6.3 9.1 11.8
============================================================
Initial mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.6 6.3 9.1 11.8
============================================================
Error estimate distribution
============================================================
█
██ █
██ █
█ █████████ ████ █ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-25) 10^(-21) 10^(-17) 10^(-13) 10^(-9)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █
█ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.8 6.8 9.8 12.8
============================================================
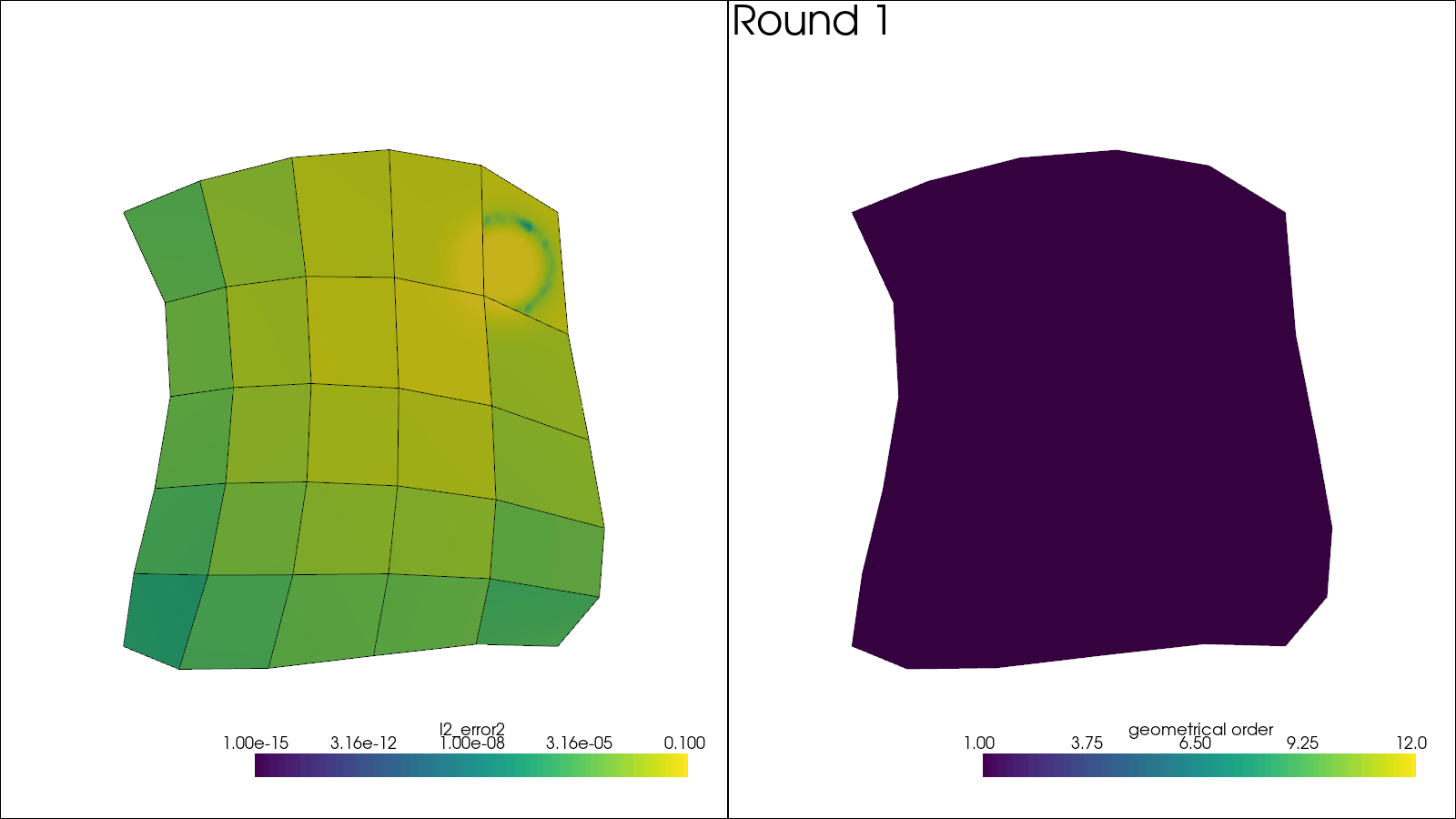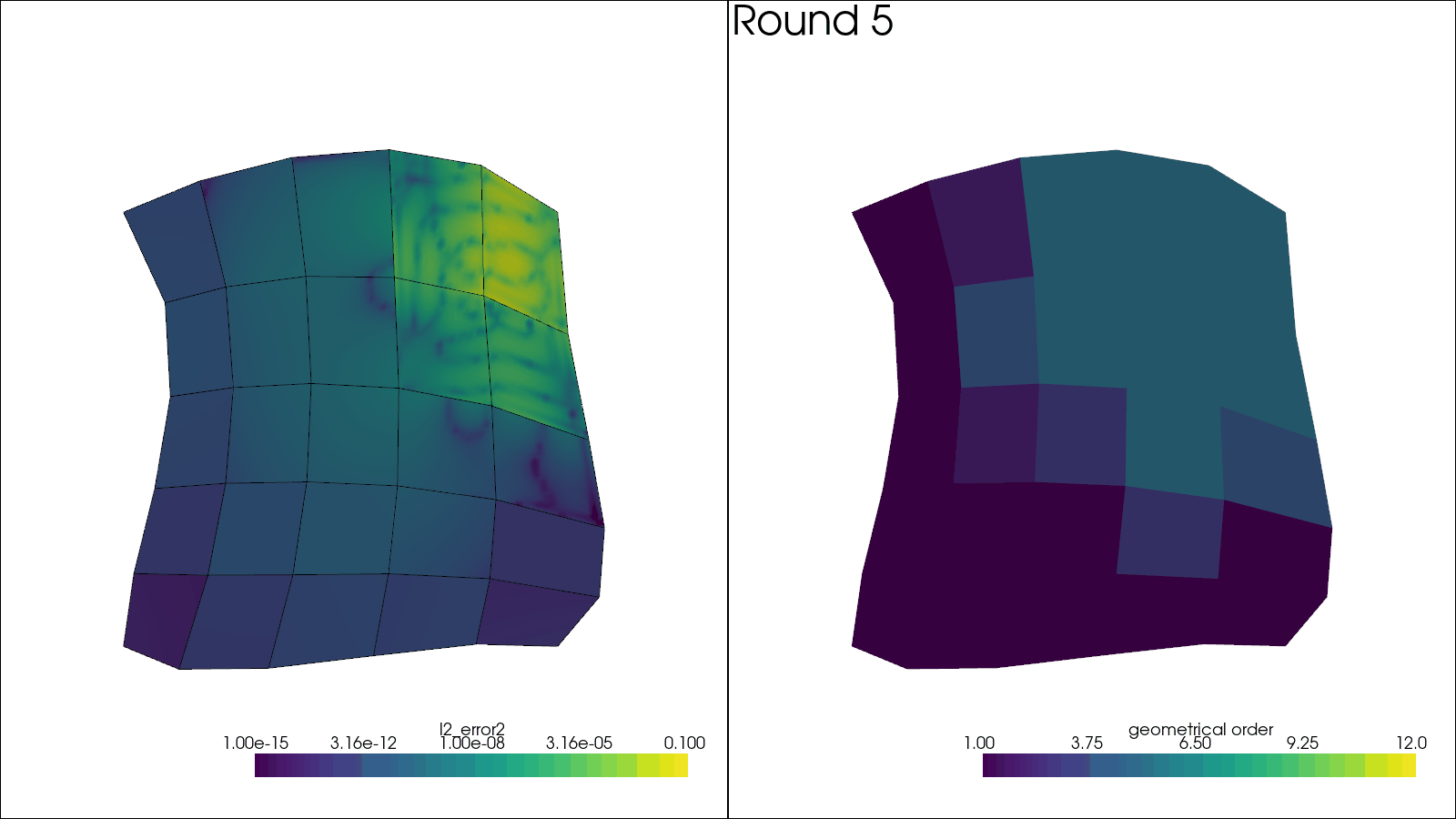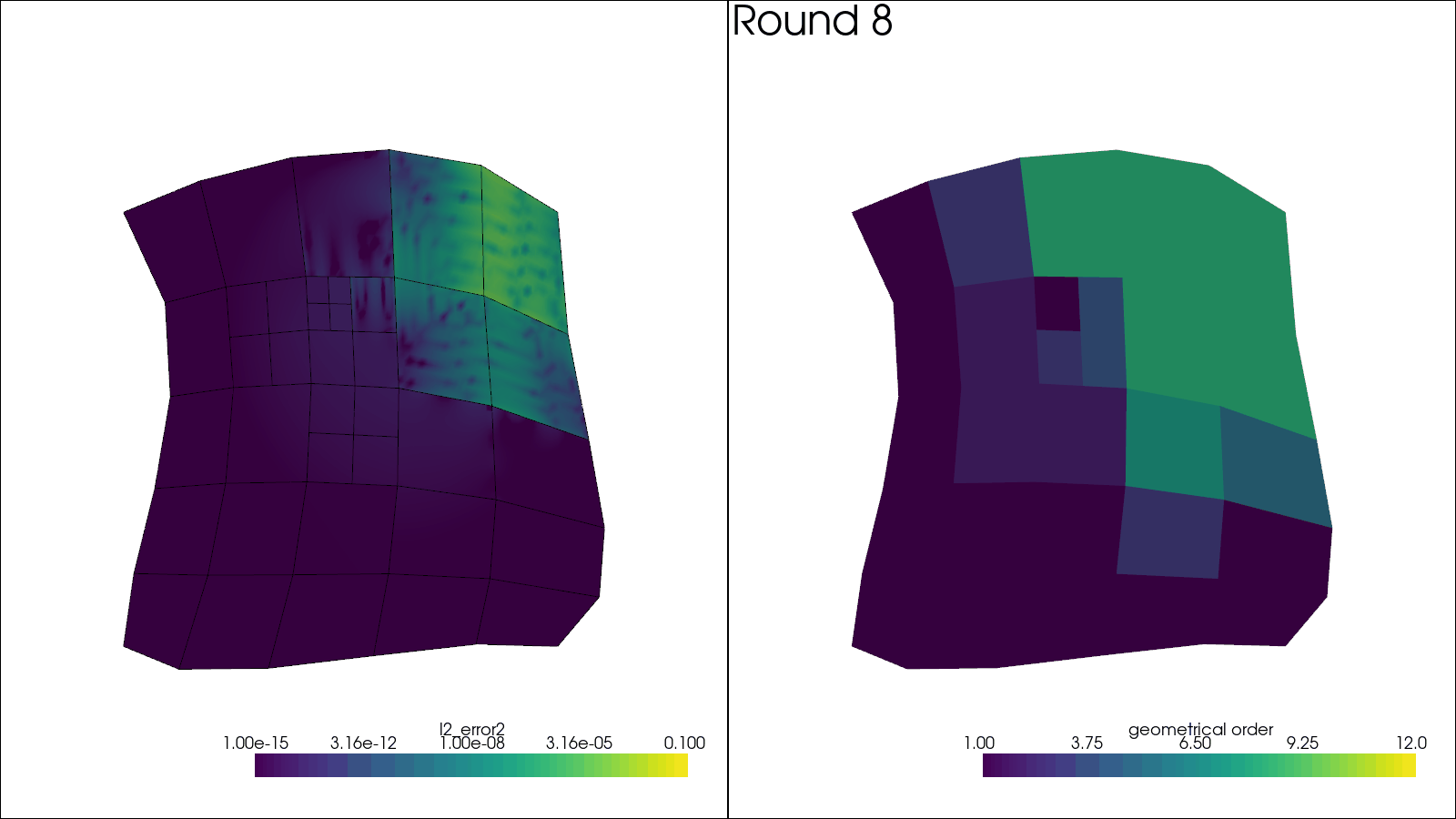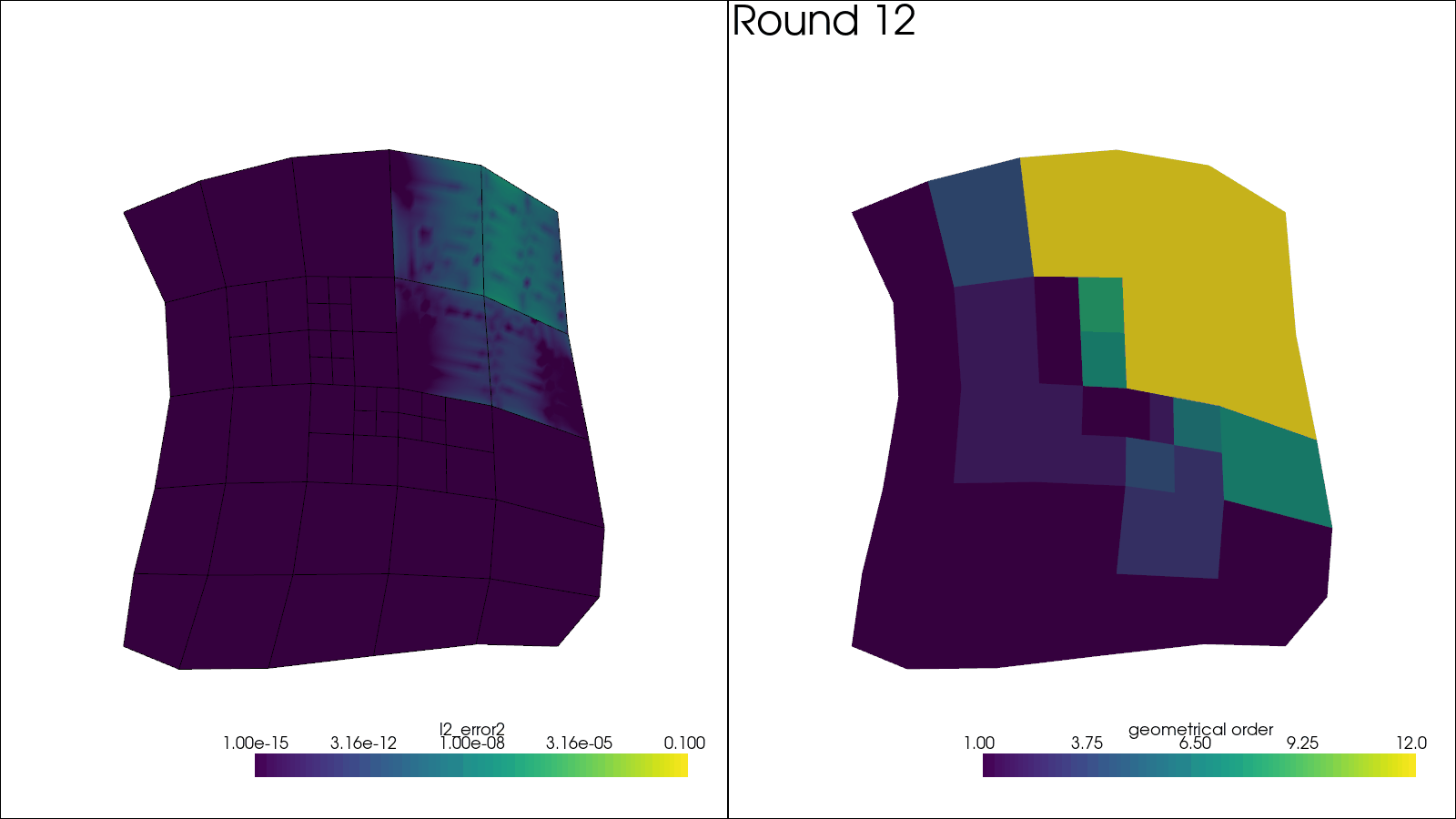
\(dp = 2\)#
errors_local_2, local_mesh_2 = run_refinement_strategy(
2, BASE_H_RATIO, BASE_ELEMENT_LIMIT, mesh_initial
)
errors_local_name_2 = err_name(2)
Initial mesh order distribution
============================================================
█
█
█
█
████████████████████████████████████████████████████████████
| | | | |
0.5 0.7 1.0 1.2 1.5
============================================================
Error estimate distribution
============================================================
█
█ █ ██ █ █
█ █ ██ █ █
█ ██ █ █ █ █ █ █ ██ █ █ █ █ █ ██
████████████████████████████████████████████████████████████
| | | | |
10^(-7) 10^(-5.7) 10^(-4.4) 10^(-3) 10^(-1.6)
============================================================
Refined mesh order distribution
============================================================
█
█ █
█ █
█ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.2 1.5 1.7 2.0
============================================================
Initial mesh order distribution
============================================================
█
█ █
█ █
█ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.2 1.5 1.7 2.0
============================================================
Error estimate distribution
============================================================
██ ██ █
██ ██ █
█ █ █ █ ███ █ █ ███ █ ███ ██ █ █
█ █ █ █ ███ █ █ ███ █ ███ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-10) 10^(-8.3) 10^(-6.2) 10^(-4.1) 10^(-1.9)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.5 2.0 2.5 3.0
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.5 2.0 2.5 3.0
============================================================
Error estimate distribution
============================================================
█
█ █ █
█ █ █
██ █ █ █ █ ███ █ █ █ █ ██ ██ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-11) 10^(-8.9) 10^(-6.7) 10^(-4.4) 10^(-2.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.7 2.5 3.2 4.0
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.7 2.5 3.2 4.0
============================================================
Error estimate distribution
============================================================
█ █ █ █
█ █ █ █
█ █ ██ █ ██ ███ ██ █ █ ██ █ █ █ █ █
█ █ ██ █ ██ ███ ██ █ █ ██ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-13) 10^(-11) 10^(-8.2) 10^(-5.7) 10^(-3.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.9 2.9 3.9 4.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.9 2.9 3.9 4.9
============================================================
Error estimate distribution
============================================================
█ █ █ █
█ █ █ █
█ █ ██ █████ █ ████ ██ █ █ █ █ █
█ █ ██ █████ █ ████ ██ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-14) 10^(-12) 10^(-9) 10^(-6.2) 10^(-3.4)
============================================================
Refined mesh order distribution
============================================================
█
█ █
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.2 3.4 4.7 5.9
============================================================
Initial mesh order distribution
============================================================
█
█ █
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.2 3.4 4.7 5.9
============================================================
Error estimate distribution
============================================================
█ █ █ ██
█ █ █ █ ██ █
█ █ █ █ ██ █
█ █ ██ ███ █ ████ ██ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-16) 10^(-14) 10^(-10) 10^(-7.4) 10^(-4.3)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.4 3.9 5.4 6.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █ █ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.4 3.9 5.4 6.9
============================================================
Error estimate distribution
============================================================
█
█ █ █
██ ███ ██
█ ███ ████ ███ ███ █ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-18) 10^(-15) 10^(-11) 10^(-8.1) 10^(-4.9)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.6 4.4 6.1 7.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.6 4.4 6.1 7.9
============================================================
Error estimate distribution
============================================================
█
█
██
█ ██ ███ █
████████████████████████████████████████████████████████████
| | | | |
10^(-19) 10^(-16) 10^(-12) 10^(-9.1) 10^(-5.6)
============================================================
Refined mesh order distribution
============================================================
█
█
█
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.9 4.9 6.9 8.9
============================================================
Initial mesh order distribution
============================================================
█
█
█
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.9 4.9 6.9 8.9
============================================================
Error estimate distribution
============================================================
█ █
███
█ ████
█ █ ██ ███████████ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-21) 10^(-18) 10^(-14) 10^(-10) 10^(-6.5)
============================================================
Refined mesh order distribution
============================================================
█
█
█
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.1 5.3 7.6 9.8
============================================================
Initial mesh order distribution
============================================================
█
█
█
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.1 5.3 7.6 9.8
============================================================
Error estimate distribution
============================================================
█
██
████
█ ██ ████ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-23) 10^(-19) 10^(-15) 10^(-11) 10^(-7.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.3 5.8 8.3 10.8
============================================================
Initial mesh order distribution
============================================================
█
█
█
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.3 5.8 8.3 10.8
============================================================
Error estimate distribution
============================================================
█
█ █ █
█ ████ ██
█ █ █████████ ████ ██ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-23) 10^(-20) 10^(-16) 10^(-12) 10^(-8.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.6 6.3 9.1 11.8
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.6 6.3 9.1 11.8
============================================================
Error estimate distribution
============================================================
█
█ █ █
█ ██ █ █
█ ██ █ ███████████ ██ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-25) 10^(-22) 10^(-17) 10^(-13) 10^(-9)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.8 6.8 9.8 12.8
============================================================
\(dp = 3\)#
errors_local_3, local_mesh_3 = run_refinement_strategy(
3, BASE_H_RATIO, BASE_ELEMENT_LIMIT, mesh_initial
)
errors_local_name_3 = err_name(3)
Initial mesh order distribution
============================================================
█
█
█
█
████████████████████████████████████████████████████████████
| | | | |
0.5 0.7 1.0 1.2 1.5
============================================================
Error estimate distribution
============================================================
█
██ ██ █ █
██ ██ █ █
█ ██ █ █ █ ██ █ ██ █ █ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-7) 10^(-5.8) 10^(-4.4) 10^(-3.1) 10^(-1.8)
============================================================
Refined mesh order distribution
============================================================
█
█ █
█ █
█ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.2 1.5 1.7 2.0
============================================================
Initial mesh order distribution
============================================================
█
█ █
█ █
█ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.2 1.5 1.7 2.0
============================================================
Error estimate distribution
============================================================
█
█ █ █
█ █ █ █
█ █ █ ██ █ █ ███ █ ██ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-10) 10^(-8.3) 10^(-6.2) 10^(-4) 10^(-1.9)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.5 2.0 2.5 3.0
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.5 2.0 2.5 3.0
============================================================
Error estimate distribution
============================================================
█
█ █ █ █
█ █ █ █
██ █ █ █ █ ███ █ █ ██ █ ██ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-11) 10^(-8.8) 10^(-6.6) 10^(-4.4) 10^(-2.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.7 2.5 3.2 4.0
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.7 2.5 3.2 4.0
============================================================
Error estimate distribution
============================================================
█ █ █ █
█ █ █ █
█ █ ██ █ ██ ███ ██ █ █ ██ █ █ █ █ █
█ █ ██ █ ██ ███ ██ █ █ ██ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-13) 10^(-11) 10^(-8.2) 10^(-5.7) 10^(-3.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.9 2.9 3.9 4.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 1.9 2.9 3.9 4.9
============================================================
Error estimate distribution
============================================================
█ █ █
█ █ █
█ █ ███ █████ ██ ███ ██ █ ██ █ █
█ █ ███ █████ ██ ███ ██ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-14) 10^(-12) 10^(-9) 10^(-6.2) 10^(-3.4)
============================================================
Refined mesh order distribution
============================================================
█
█ █
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.2 3.4 4.7 5.9
============================================================
Initial mesh order distribution
============================================================
█
█ █
█ █ █
█ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.2 3.4 4.7 5.9
============================================================
Error estimate distribution
============================================================
█
█ █ █ █
█ █ █ █ ██ █ █
█ █ ██ ███ █ ████ ██ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-16) 10^(-14) 10^(-10) 10^(-7.4) 10^(-4.3)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █ █ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.4 3.9 5.4 6.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █ █ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.4 3.9 5.4 6.9
============================================================
Error estimate distribution
============================================================
█ █
█ █ █
██ ███ ██
█ ███ ████ ███ ██ █ █ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-18) 10^(-15) 10^(-11) 10^(-8.1) 10^(-4.9)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.6 4.4 6.1 7.9
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.6 4.4 6.1 7.9
============================================================
Error estimate distribution
============================================================
█
██
█ ███
█ ██ ███ ███████ █ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-19) 10^(-16) 10^(-12) 10^(-9) 10^(-5.6)
============================================================
Refined mesh order distribution
============================================================
█
█
█
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.9 4.9 6.9 8.9
============================================================
Initial mesh order distribution
============================================================
█
█
█
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 2.9 4.9 6.9 8.9
============================================================
Error estimate distribution
============================================================
█ █
███
█ ███ █
█ █ ██ ███████████ █ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-21) 10^(-18) 10^(-14) 10^(-10) 10^(-6.5)
============================================================
Refined mesh order distribution
============================================================
█
█
█
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.1 5.3 7.6 9.8
============================================================
Initial mesh order distribution
============================================================
█
█
█
█ █ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.1 5.3 7.6 9.8
============================================================
Error estimate distribution
============================================================
█
██
█ ████
█ ██ ████ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-23) 10^(-19) 10^(-15) 10^(-11) 10^(-7.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.3 5.8 8.3 10.8
============================================================
Initial mesh order distribution
============================================================
█
█
█
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.3 5.8 8.3 10.8
============================================================
Error estimate distribution
============================================================
█
█
█ ███ ██
███████ ██ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-25) 10^(-21) 10^(-17) 10^(-12) 10^(-8.2)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.6 6.3 9.1 11.8
============================================================
Initial mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.6 6.3 9.1 11.8
============================================================
Error estimate distribution
============================================================
█
█ █ █
██ ██ █
█ ██ █ █████████████████ █ █ █ █
████████████████████████████████████████████████████████████
| | | | |
10^(-25) 10^(-22) 10^(-17) 10^(-13) 10^(-9)
============================================================
Refined mesh order distribution
============================================================
█
█
█ █
█ █ █
████████████████████████████████████████████████████████████
| | | | |
1.0 3.8 6.8 9.8 12.8
============================================================
Plotting Results#
def plot_error_rates(*args: tuple[str, npt.ArrayLike]) -> None:
"""Plot a comparison of convergence rates with their names."""
fig, ax = plt.subplots(figsize=(10, 5))
for label, data in args:
el = np.array(data)
err = el[:, 1]
ns = el[:, 0] / 100
kl1, kl0 = np.polyfit(ns, np.log(err), 1)
kl1, kl0 = np.exp(kl1), np.exp(kl0)
ax.scatter(el[:, 0], err, marker="x")
ax.plot(
el[:, 0],
kl0 * kl1 ** (ns),
label=label
+ f": ${kl0:.3g} \\cdot {{{kl1:.3g}}}^{{\\frac{{N_\\mathrm{{dofs}}}}"
f"{{100}}}}$",
linestyle="dashed",
)
ax.grid()
ax.legend()
ax.set(
xlabel="$N_\\mathrm{dofs}$",
ylabel="$\\left|\\left| u - \\bar{u} \\right|\\right|_{L^2}$",
yscale="log",
)
fig.tight_layout()
plt.show()
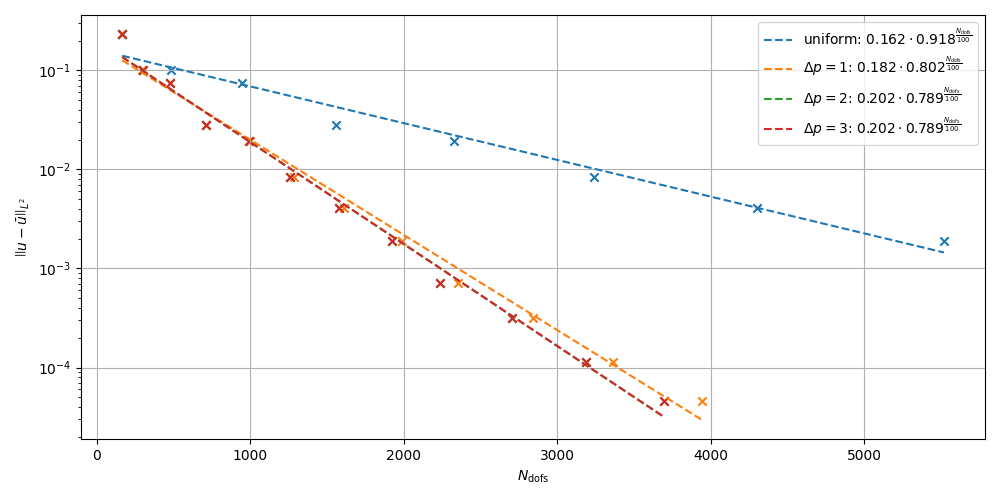
plot_error_rates(
("uniform", errors_uniform),
(errors_local_name_1, errors_local_1),
(errors_local_name_2, errors_local_2),
(errors_local_name_3, errors_local_3),
)
Compare the Meshes#
plot_mesh_comparisons(
("Baseline", mesh_initial),
(errors_local_name_1, local_mesh_1),
(errors_local_name_2, local_mesh_2),
(errors_local_name_3, local_mesh_3),
)

Total running time of the script: (1 minutes 44.986 seconds)